Interaction of Light with Matter

Introduction

The usual treatment of quantum mechanics uses time-independent wavefunctions with the Schrödinger equation to determine the energy levels (eigenvalues) of a system. To understand the interaction of light (electromagnetic wave) and matter, we must think about the time dependent case. consider we need to concern ourselves with how these interact with electromagnetic waves. Such interactions are at the very heart of spectroscopy. There are lots of spectroscopic processes. The important ones are:
 
  • absorption
  • resonance fluorescence
  • relaxed fluorescence
  • refraction
  
  • Rayleigh scattering
  • Brillouin scattering
  • Raman scattering
  • resonance Raman scattering

These processes appear to be different but in fact they are all closely related. We would like to examine these in much greater depth to understand them and their relationships.

A Simple Analogy

The most naive way to discuss absorption and emission of light is to consider the atom and its electrons as electrons on springs. You might object and say that is a ridiculous comparison and it is. However, the mathematics are identical and a great deal of insight can come from the analogy. If you have a weight on a spring, you can set it into motion by tapping it at its natural resonance frequency. The best way to input energy to it is to tap it 90 degrees out of phase. We can diagram the experiment as follows:

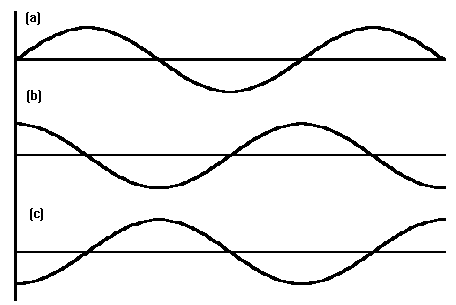
Curve (a) represents the oscillatory behavior of the spring, curve (b) is the applied force that is required to make it oscillate and curve (c) is the applied force that is required to stop it from oscillating. In (b) the spring is absorbing energy and in (c) it is providing energy. (b) represents absorption and (c) represents stimulated emission. The only difference is the phase - 180 degrees to be exact. Both (b) and (c) are out of phase with (a).

Our description so far has applied only to a driving force in resonance with the vibrational frequency of the spring. What happens out of resonance? If the driving frequency is lower than resonance, there will be an in-phase component of the oscillation. If it is higher, there will be a 180 degree out-of-phase component. If the driving force is a cosine function, the oscillation will have a sine functionality at resonance and an additional cosine functionality at higher or lower frequencies.

A Real Atom or Molecule

Now what happens if we apply an electric field to a real atom or molecule? The electric field will distort or polarize it. We can represent that distorted wavefunction as a linear combination of all the wavefunctions of the atom. (Actually, that isn't quite true. Only the states with opposite parity will contribute. Do you know why?) If we reverse the direction of the field, the distortion will also reverse. If we do that often at a frequency that matches a transition in the atom or molecule, the distortion or polarization will build up. An isolated atom or molecule doesn't suffer any losses and therefore the distortions can become extremely large. Quantum mechanically, one describes this problem by saying that an excited state gets mixed into the ground state by the applied electric field and that this mixing is time dependent since the field is. We could draw a picture of this oscillation for the H atom when there are an equal amount of 1s and 2p orbitals mixed into this transition state. This case corresponds to the situation when the distortion (or dipole moment) is the largest.

A series of contour plots representing the temporal behavior:

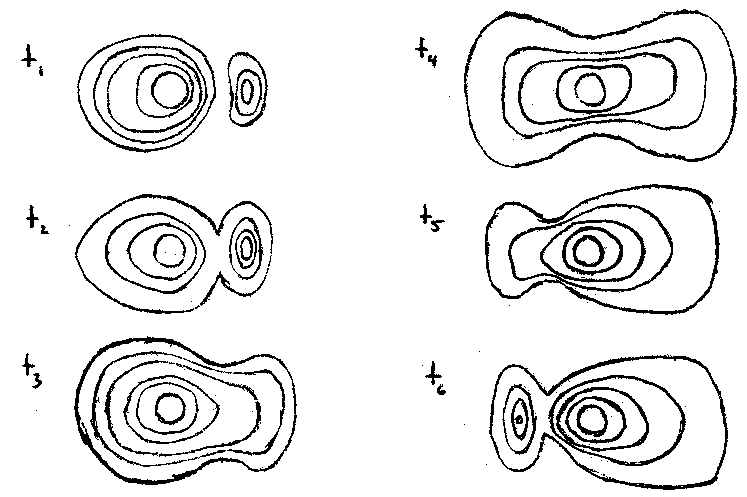
We start at t1 with a state that is primarily 1s and progress to a state at t4 that is primarily 2p and then back again. Quantitatively, we could use the time-dependent wave equation and derive a correct time dependent wavefunction for a two-state system that is interacting with an incoming electromagnetic wave whose frequency was w.

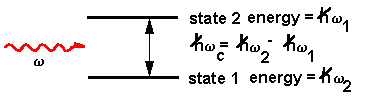
The Hamiltonian representing the interaction of the electric field, E, of the incoming wave with the dipole moment of the atom, µ, is:

H = µ E cos w t

The wavefunction as a function of time is then: (sorry too complicated for HTML)

Spectroscopy

After the driving field has been applied for a long time, the effects we have been discussing will die out. They are only transients. They die out because there will always be interactions that will dephase molecules so they lose coherence with the driving field. Nevertheless, there will be a steady-state polarization that will have an in-phase and an out-of-phase component. If we are at resonance, we saw there was only an out-of-phase component. If we are very far from resonance, there is only an in-phase component. As an electromagnetic wave travels through a material, it induces a polarization whose oscillation launches an electromagnetic wave of its own which adds to the incoming wave. Since there can be an out-of-phase component to this new wave, the net result is a phase shift in the emerging wave. This phase shift is the index of refraction of the material. Large phase shifts correspond to large indices of refraction. If the material is completely uniform and ordered, all of the oscillating dipoles will be related to each other by the phase and frequency of the light. The net electromagnetic field formed by the sum of all of them will add only in the direction of the propagation of the light and will destructively interfere at all other angles and all other directions. However, if there are regions where the material is not of uniform density (and in fact no material at a finite temperature can have a uniform density), then there will be some dipoles which do not contribute to the net electromagnetic field and light can be scattered in other directions. This scattering is Rayleigh scattering. If the density fluctuations are static, the scattered light will have the same frequency as the incoming light. If the density fluctuations are dynamic, the scattered frequency will be shifted by an amount that depends upon the frequency of the density fluctuations. Particular density fluctuations associated with propagating vibrations in solids (phonons) have unique frequencies and give rise to scattering at a frequency shifted from the input frequency by that of the phonon. This scattering is Brillouin scattering. Typically the shifts are in the region of 0.1 to 1 cm-1.

As an electromagnetic field propagates through a sample, there will be a certain average excited state population that will have a coherent and an incoherent component. At all times, the excited state has the option of simply relaxing spontaneously and emitting a photon. This process is spontaneous emission and is incoherent relative to the driven polarization. If the spontaneous emissions occurs from the coherent excited state population, the emission is called Raman scattering. The state it relaxes to can be a different electronic state in which case it is electronic Raman scattering, a different vibrational state where it is vibrational Raman scattering (or just Raman scattering), or a different rotational state where it is rotational Raman scattering. The emitted light frequency will differ from the exciting frequency by the energy of the final state. Quantum mechanically, Raman scattering is diagrammed by:

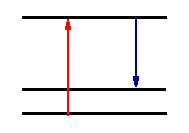
The top dotted line represents the coherent oscillating state. We know what that looks like. It is simply the atom or molecule distorted by the electric field of the incoming light wave. In a real system, it doesn't usually correspond to a particular stationary state of the molecule and since one doesn't usually want to have to derive the eigenfunctions that describe the state, we instead simply express it as a linear combination of all the states required to make this distorted state. It is called a virtual state because there is no real state at that energy usually. But we know it is simply the distorted molecule. Notice that the importance of Raman scattering depends upon how easily the molecule is distorted. Classically, this property is measured by the polarizability of the molecule and therefore polarizability determines the amount of Raman scattering.

Things become very interesting when the incoming electromagnetic wave approaches an electronic resonance. There is now the possibility of achieving a finite incoherent excited state population as well as a coherent population. The distortions of the molecules will become much larger near electronic resonances. Spontaneous emission will still occur from both the coherent and incoherent excited state populations which will now be considerably larger than when the driving frequency was far from resonance. The emission from the coherent population will be resonantly enhanced Raman scattering (resonance Raman) while the incoherent population will cause normal fluorescence. There will also be losses from the excited state population due to nonradiative relaxation. All of these losses result in absorption of light.

The relative amounts of resonance Raman and fluorescence depends upon the relative coherent and incoherent excited-state populations. This in turn depends upon the relaxation effects that are important in the system. In most molecular systems, dephasing by collisions or other interactions is a dominant factor in determining the incoherent population. The ratio of fluorescence to Raman will be approximately 2 / (T2 · γ) where T2 is the dephasing time constant and γ is the radiative rate of spontaneous emission.

The fluorescence that one observes can also have different character. If the fluorescence originates from an incoherent population that has been formed by dephasing, emission to the ground state will be resonance fluorescence and will have a lifetime characteristic of the emitting state. The linewidth of the emission will reflect the widths of the initial and final states. In contrast, the resonance Raman emission will cease when the excitation source is turned off and will have an emission linewidth characteristic of the final state. It is also possible that the incoherent excited population can be formed from relaxation from the state that was connected to the ground state. This fluorescence is relaxed fluorescence and is generally shifted in wavelength.

Either fluorescence or resonance Raman can be quenched. If there are rapid nonradiative relaxation processes that depopulate the incoherent excited state population, the fluorescence will be quenched. One would then see only the resonance Raman. (The resonance Raman intensity could also be lowered.) If there were rapid dephasing or relaxation processes that depopulated the coherent populations, the resonance Raman emission would be quenched. For example, one can observe strong Raman scattering many times when the v = 0 to v = 0 electronic transition is excited but very little when the v = 0 to v = n transitions are excited because the vibrational states relax very quickly to the unexcited vibrational state. Then the excitation profile of the resonance Raman effect will not follow the absorption profile for the molecule.

Adapted from lecture notes by Prof. John Wright, Univ. of Wisconsin.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.