![]() y
= Eyy
y
= Eyy
The electron moves between two walls at x=0 and x=L. The potential energy of the particle is zero between the walls and infinity at the walls. What this statement is saying is that the particle can only be between x=0 and x=L.
V= ¥ V=0 V= ¥ //////| |\\\\\\ //////| |\\\\\\ //////| |\\\\\\ //////| |\\\\\\ //////| |\\\\\\ //////| |\\\\\\ //////| |\\\\\\ //////+--------------------+\\\\\\ 0 L x -->By classical mechanics we could roll a particle along the x-axis in this box and predict its position at any later time. That is not true for a particle in the quantum regime. The behavior of a particle is completely specified quantum mechanically by the Schrödinger equation:
![]() y
= Eyy
y
= Eyy
where is the Hamiltonian that describes the system, and y and E are eigenfunctions and eigenvalues, respectively, that satisfy this equation.
For any particle, the total energy of that particle is the sum of the
kinetic and potential energy. For the one-dimensional case ![]() is:
is:
![]() =
p²/2m + V (x)
=
p²/2m + V (x)
Thus, for a particle in one dimension (x-axis) the Schrödinger equation is:
- [(h² d²)/(8π² m dx²) +V]y = Ey
where:
h is Planck's constant,
m is the mass of the particle (an electron in this
case), and
V is the potential energy.
Since V = 0 in the box, this equation simplifies to:
− (h² d²y)/(8π²m dx²) = Ey
The general solution for this type of differential equation is:
y(x) = A sin(kx) + B cos(kx)
We can use the boundary conditions and physical reality to narrow down the solution. Since y = 0 at x = 0, the cos term is not reasonable and we get:
y = A sin(kx)
yn = A sin(nπx/L)
n is an integer greater than zero we call a quantum number.
(n = 0 → no particle in the box)
The electron must be somewhere in the box so normalize to find A.
probability = oò¥y² dτ
o ∫Ly² dx = 1
o ∫L A² sin²(nπx/L)dx = 1
A = Ö(2/L)
We now have our allowed wavefunctions:
yn = [Ö(2/L)] sin(nπx/L)
Substituting yn into the Schrödinger equation gives the allowed energies:
En = n²h²/8mL² for n = 1, 2, 3, ...
Look at this result: Wave properties and boundary conditions lead to quantized energies.
Note that as the size of box changes the energies change proportional to 1/L². As the box shrinks, the possible energies of the particle increases (see the example below).
For large quantum numbers (needed for reasonable energies at macroscopic
dimensions) the spacing between nodes in the wavefunctions become too small
to measure. The result is that the particle has an equal probability of
being anywhere in the box. Similarly, the relative difference in energy
between levels large becomes too small to measure, so the energy the particle
can have appears continuous rather than quantized when n becomes. Both
position and energy can be described by classical mechanics at large n.
This result is called the Bohr Correspondence Principle.
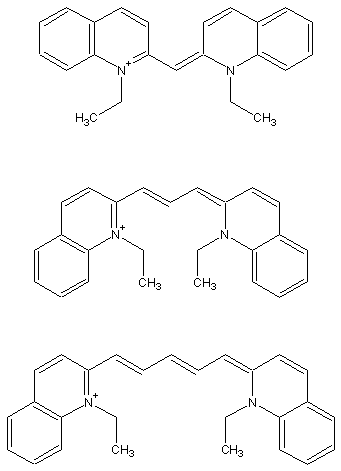
reference: G. M. Shaloub, J. Chem. Ed. 1997, 74, 1317.
Remember that in spectroscopy we are measuring the differences in energy between levels.
ΔE = h²(nu² − n1²)/8mL²
N = number of π electrons. Since two electrons occupy each orbital the number of populated levels is N/2.
ΔE = h²/8mL²[(N/2 + 1)² − (N/2)²]
ΔE = h²/8mL² (N + 1)
λ = 8mL²/h(N + 1)
assume L = (2k+2)b, where:
k = number of double bonds along the chain
b = 139 pm (C-C length in benzene)
| L (pm) | Theory | Experiment | |
| cyanine | 556 | 328 nm | 523 nm |
| pinacyanol | 834 | 453 nm | 605 nm |
| dicarbocyanine | 1112 | 580 nm | 706 nm |
The simple one-dimensional particle-in-the-box model does not match the experimental results exactly, but it does show the same trend of decreasing energy (longer wavelength) as the "box" gets larger. You can try refining the assumptions of the model to get a closer match to the experimental data.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.