Successful LCAO

To combine successfully arbitrary atoms A and B with the LCAO approach Ψ = c_AΦ_A + c_BΦ_B, the wave functions Φ_A and Φ_B need to have the same symmetry with respect to the axis of the emerging molecule. This results from the fact that no combination of Φ_A and Φ_B is possible in cases where S and therefore β as well become zero and we get two independent equations with the solutions E = α_A, Ψ = Φ_A and E = α_B, Ψ = Φ_B. This happens for two atomic orbitals that do not overlap at all or for pairs of orbitals Φ_A and Φ_B where symmetry allows to separate the integrals for S and β into two parts with identical, but contrarily signed values that eventually yield zero. In such cases, it is said that Φ_A and Φ_B do not combine for symmetry reasons and there is no MO where both wave functions appear together.

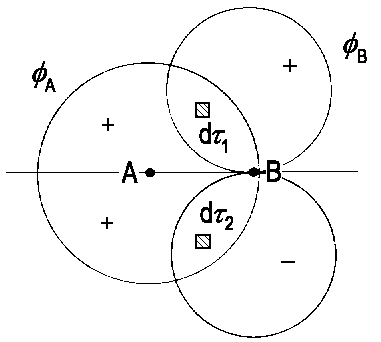An example is depicted in the figure on the left, where ΦA is an s-AO and ΦB is an px-AO. Axis x is assumed to be orthogonal to the axis of the molecule AB which is in accordance with a convention saying that the molecule's axis points in direction z. The figure illustrates that, due to contrary signs of the wave function in both lobes of the px orbital, the integral S = ∫ΦAΦBdτ = 0. Obviously, combinations of an px- orbital with an py-, pz- or an s-orbital of another atom are not relevant for molecular bonding. In case the integral ∫ΦAΦBdτ is zero, the pair of wave functions ΦA and ΦB are said to be orthogonal. As shown above, different symmetry with respect to a plane that contains both nuclei causes wave functions to be orthogonal.

The integral ∫ΦAΦBdτ disappears due to symmetry as for any volume element dτ1 there is a respective element dτ2. The integrand delivers identical, but contrarily signed values for such pairs of volume elements.

The following table classifies combinations of s-, p- and d-type atomic orbitals in view of the LCAO molecular orbital approach.

In later chapters, examples for combinations of one atomic orbital Φ_A with two or more orbitals Φ_B of atom B are presented. Again, possible partner orbitals are found in column "combines with Φ_B". As we regard axis z as molecular axis, preferable d-orbitals are d_xy, d_yz, d_zx, d_z² and d_x²-y².

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.