With acrolein as example, Hückel's method to calculate molecular orbitals and the results are explained. (chapter based on a work by Dr. Horst Bögel).
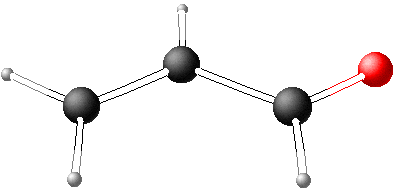
First, we build a secular determinant which describes the structure of acrolein. The atomic parameter are found within the diagonal, for a carbon atom, x is inserted, for heteroatoms X the sum x+hX. The value 1 is inserted for C-C bonds, a value kC-X for C-X bonds. For the majority of cases, the needed values for hX and kC-X can be taken from the table below.
| X | hX | C-X | kC-X | |
|---|---|---|---|---|
| F | 2.84 | C-F | 0.68 | |
| Cl | 1.45 | C-Cl | 0.57 | |
| Br | 1.16 | C-Br | 0.38 | |
| J | 0.78 | C-J | 0.19 | |
| :O | 2.06 | C-O: | 1.31 | |
| :O-CH3 | 1.96 | C=O | 1.93 | |
| .O | 1.18 | C-N: | 1.30 | |
| :N | 1.47 | C=N. | 1.06 | |
| .N | 0.83 | C-CH3 | 0.18 | |
| :CH3 | 0.88 | N-O | 1.95 | |
| from: G. DERFLINGER, H. LISCHKA: Mh. Chemie 100 (1969) 1003 | ||||
| Acrolein's secular determinant is |
|
Transformation of this determinant yields an equation of the fourth degree:
x4 + 1.18 x3 - 5.725x2 - 2.36x + 3.725 = 0
The zeros of this equation or, respectively, the eigenvalues of the determinant are
| x1 = -2.7654 | x2 = -1.0207 | x3 = 0.6880 | x4 = 1.9182 |
The four eigenvalues and the following equation yields the energy levels of the molecular orbitals
Ei = α - xi β-
|
These levels are shown in the diagram here. Empiric values are α= -11 eV and β= -2.5 eV. The total energy of the molecule equals the sum of the electrons' energies in the respective molecular orbitals. The total energy of the π-electrons is E = ∑i=1 bi⋅Ei where bi represents the occupancy of orbitals with the values 0 (empty), 1 and 2 (pair of electrons). |
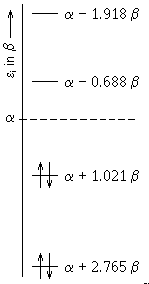
|
E = 2(α+2.7654β)+2(α+1.0207β) = 4α+7.5722β = -25.0695 eV
∑R=1 (hRS-EiδRS) ciR = 0
If there is a bond R-S,
then hRS =βRS, otherwise hRS = 0
and αRS = 1 for R=S, otherwise RS = 0.
The following table contains the results:
| MO 1 | MO 2
HOMO |
MO 3
LUMO |
MO 4 | |
|---|---|---|---|---|
| eigenvalue | -2.7654 | -1.0207 | 0.6880 | 1.9182 |
| atom 1 | 0.0919 | -0.6593 | -0.6990 | -0.2613 |
| atom 2 | 0.2542 | -0.6730 | 0.4809 | 0.5012 |
| atom 3 | 0.6111 | -0.0276 | 0.3682 | -0.7002 |
| atom 4 | 0.7439 | 0.3341 | -0.3804 | 0.4362 |
The obtained molecular orbitals are depicted below:
| MO Ψ12 | 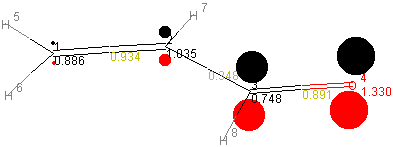 |
| MO Ψ22 (HOMO) | 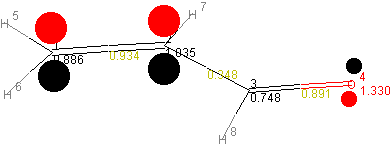 |
| MO Ψ32 (LUMO) | 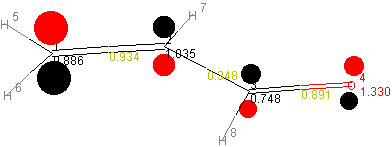 |
| MO Ψ42 | 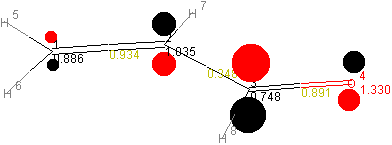 |
| occupancy: | Ψ12 | Ψ22 | Ψ30 | Ψ40 |
|---|
The formula
qR = pRR = ∑i bi ciR²
andpRS = ∑i bi ciR ciS
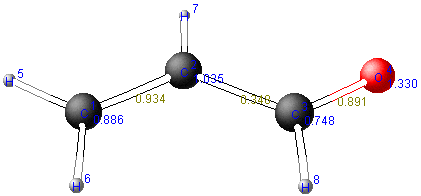
allow to establish a p-matrix that, in turn, serves to construct a molecule diagram.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0.8863 | |||
| 2 | 0.9342 | 1.0351 | ||
| 3 | 0.0 | 0.3479 | 0.7485 | |
| 4 | 0.0 | 0.0 | 0.8909 | 1.3302 |
The values within diagonal of the matrix indicate the electron density (pRR) near the respective atoms.
Example: density of electrons near carbon atom C(2)
pRR = 2 * (0.2542)2 + 2 * (0.6730)2 + 0 * (0.4809)2 + 0 * (0.5012)2 = 1.0351
The formal charge of any atom is: QR = NR - pRR.
Besides the diagonal of the matrix, the bond order appears.
Example: bond order for the π-bond C=O between carbon and oxygen
pRS = 2 * (0.6111 * 0.7439) + 2 * (0.0276 * -0.3341) + 0 * (0.3682 * -0.3804) + 0 * (-0.7002 * 0.4362) = 0.8909
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.