Energy Levels of MOs in Homonuclear Molecules

The sequence of molecular orbitals with respect to their energy is fundamental to introduce a principle for the allocation of electrons to molecular orbitals. The currently available data support the following succession of molecular orbitals:

Note that any molecular orbital of type π is doubly degenerated. For elements of the second row of the periodic table that form diatomic molecules, the σ_g-MO is always below the π_u-MO.

The energies of MOs are often discussed with reference to a correlation diagram. It shows these energies against the internuclear distance R. For high values of R, the molecular orbitals become atomic orbitals of single atoms; for R → 0 they approach the atomic orbitals of an "united atom" that emanates from an imaginary fusion of the nuclei of both atoms. Thus, molecular orbitals are treated as a hypothetical intermediate between two extremes already described in the basic theory of atomic orbitals. The correspondence between AOs of the one and the other extreme is founded on the criteria of energy and symmetry. To find corresponding orbitals, first the AOs are listed in accordance with an increase of energy. Second, orbitals of matching symmetry are connected. The dashed lines between the energy levels indicate these correlations. Note that in such diagrams, no crossing points of lines that represent orbitals of the same symmetry exist. This reflects the non-crossing rule, of which the background is treated in detail here. Furthermore, the already familiar categories of bonding and antibonding MOs have their counterpart in the connection's slope: There are rising and falling lines. Fig.1 shows a typical correlation diagram for a homonuclear diatomic molecule.

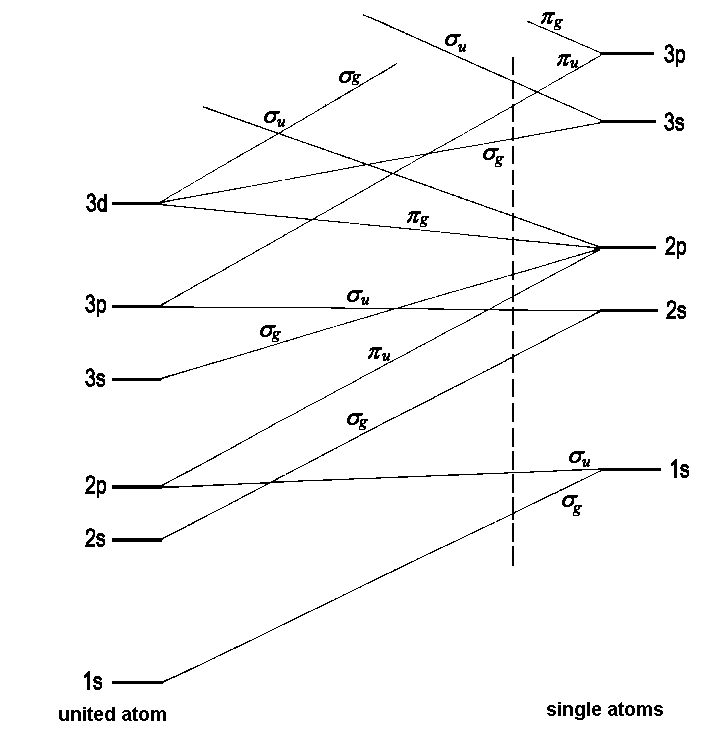Fig.1: Determination of molecular orbital energies by means of a correlation diagram. For a certain distance indicated by the vertical line, the sequence of MO energies is obtained from the diagram.

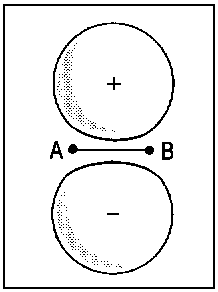
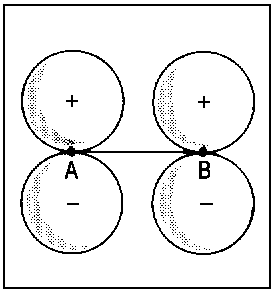
The concept of correlation is exemplified in Fig. 2 for the transition of 2p_x atomic orbitals of single separate atoms (right). When the nuclei A and B approach each other (R → 0), the molecular orbitals 1π_u and 1π_g (middle) are obtained. For R = 0, the lower extremity is reached and it is possible to describe the the former 1π_u orbital as 2p_x and the former π_g orbital as 3d_zx (left). Keep the limitations of the approach in mind. E.g. dissociation of the ionic molecule H₂⁺ actually yields one hydrogen atom and one proton. In contrast, for R → ∞, the MO approach will hold to an electron that is distributed in a molecular orbital described by a symmetric wave function.

2px		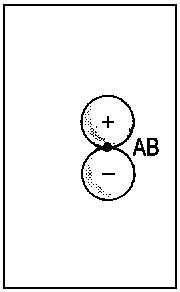		2pxA+2pxB
3dzx		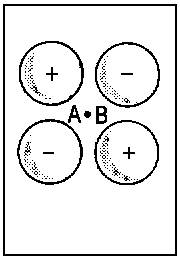		2pxA-2pxB
	united nuclei		separate atoms
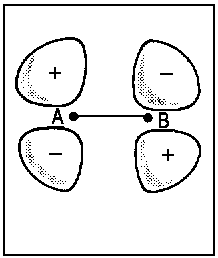
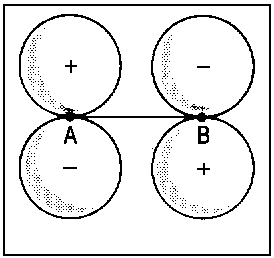
Fig.2: Example for the correlation of orbitals for homonuclear diatomic molecules. Three internuclear distances R are shown. The upper row reveals the correspondence between the πu molecular orbital and a p-type atomic orbital of an assumed atom formed by fusion of the nuclei A and B. The lower row illustrates the same correspondence for the πg molecular orbital and an orbital of type dzx. Due to the highly charged centre of the united atom, the respective orbitals are quite compact.

Actually, the MOs appear more complicated than a linear combination of two AOs like 2s_A+2s_B. For example, the 2σ_g and 3σ_g MO would be described more accurately by:

2σ_g : c₁₁ (2s_A + 2s_B) + c₁₂ (2p_zA − 2p_zB)
3σ_g : c₂₁ (2s_A + 2s_B) + c₂₂ (2p_zA − 2p_zB)

Orbitals of σ_u-type are to be obtained in a similar way. Take care of the symmetry of wave functions when using linear combinations of atomic orbitals. Only combinations of wave functions of identical symmetry are reasonable.

Fig. 3 qualitatively shows the energy of molecular orbitals. The interactions between the AOs causes the energy levels to split. In addition, interaction between emerging MOs of one symmetry and similar energy further increases the distance found between the levels. Therefore, an 1π_u can be lower in energy than a 3σ_g molecular orbital.

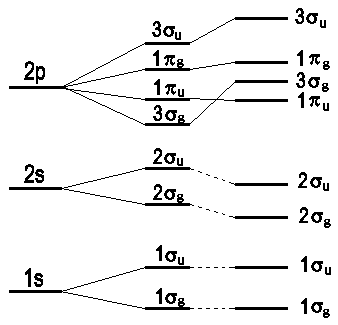Fig.3: Sequence of MO levels: Obtained from an approach with two AOs (in the middle) Obtained when using the more accurate approach above, where four AO wave functions are combined (on the right side).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.