Symmetric Top

Examples: CH₃I, C₆H₆, NH₃

If we denote I_|| as the moment of inertia parallel and I_⊥ orthogonal to the molecule's axis, we have two cases: For I_|| < I_⊥ we have a rotator similar to a record which is said to be of oblate type. Otherwise, with I_|| > I_⊥ the rotor is of prolate type that may remind us of a cigar. Within the world of atoms and molecules, benzene is an example for the first, methyliodide an example for the latter. For both types, the rotational energy is composed of two components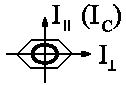

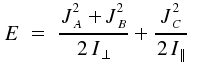
The transition to quantum mechanics is eased by the fact that the energy values respective J² and one selected axis are recieved simultaneously. For J², which is

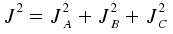
the energy values are defined by

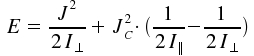
We now replace the square of the angular momentum by the eigenvalues of the quantum mechanical angular momentum operator J² → J(J+1)h² and use K for the eigenvalues that correspond to a projection of the momentum onto the molecules axis (i.e. J_CΨ → KhΨ). For the quantum mechanical energy levels, we finally obtain:

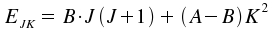K = 0, ±1, ±2, ..., ±J
J = 0, 1, 2, ...

B = h/(4πcI_⊥)
A = h /(4πcI_||)

We now consider two extreme cases of a rotating symmetric top

Obviously, the sign of K does not affect the energy as it is dependents on the square of K. Therefore, all levels are doubly degenerate. But as there are the 2J+1 additional possibilities for angular momentum, respective of an external axis (M_J = 0, ± 1, ± 2, ± 3, ... ± J), the energy level of a symmetric top is but 2(2J+1)-fold degenerate. For K = 0 we have the exception of (2J+1)-fold degeneracy. Though there is no definition for clockwise/anti-clockwise and +/−, the sign indicates two possibilities of rotation with identical energy.

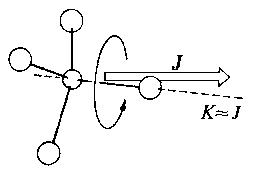
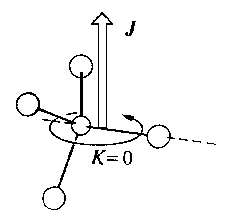
a) around the molecule's axis b) perpendicular to the molecule's axis

For the first extreme with |K| = J, where J reaches a maximum with respect to the molecules's axis, the rotation is mainly around this axis and rotational constant A (resp. I_||) is decisive for the energy levels.

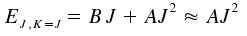
For the other extrem of K = 0, the molecule rotates perpendicular to its axis. Therefore, the projection of the angular momentum on the axis is zero and the rotational energy becomes

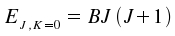
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.

We now consider two extreme cases of a rotating symmetric top
		Obviously, the sign of K does not affect the energy as it is dependents on the square of K. Therefore, all levels are doubly degenerate. But as there are the 2J+1 additional possibilities for angular momentum, respective of an external axis (M_J = 0, ± 1, ± 2, ± 3, ... ± J), the energy level of a symmetric top is but 2(2J+1)-fold degenerate. For K = 0 we have the exception of (2J+1)-fold degeneracy. Though there is no definition for clockwise/anti-clockwise and +/−, the sign indicates two possibilities of rotation with identical energy.
a) around the molecule's axis	b) perpendicular to the molecule's axis