Matrix representation of symmetry operations

 

Using carthesian coordinates (x,y,z) or some position vector, we are able to define an initial position of a point or an atom.

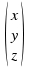
The initial vector is submitted to a symmetry operation and thereby transformed into some resulting vector defined by the coordinates x', y' and z'. In an algebraic context, this transformation is expressed a matrix which processes the initial position vector. We write

final vector = Matrix * initial vector.

The most primitive symmetry operation is the identity and yields a final vector identical to the initial vector. It is the unity matrix or identity matrix which leaves all coordiates unaffected.

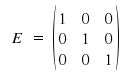
If we want to perform a reflection on the xy-plane (analogous to a horizontal plane σ_h), coordinate z changes the sign.

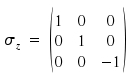
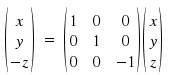
The matrices which are applied for performing a reflection on the yz-plane and xz-plane are the matrices σ_x and σ_y respectively.

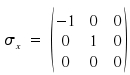
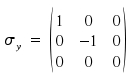
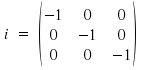
The inversion i relates the coordinates (x,y,z) with (-x,-y,-z) and is connected with the following matrix:

Obviously, a twofold application of the inversion matrix yields the coordinates of the initial point (x,y,z) which is reflected by E = i*i.

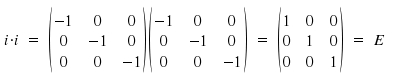
The matrix for a rotation about axis z by an arbitrary angle Θ is derived easily if we imagine two two-dimensional coordinate planes with identical origin but an angular difference of Θ between the axes. In our context of symmetry, we just need to deal with the discrete values of Θ = 2π/n for the angle of rotation.

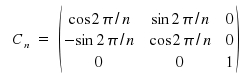
The matrices for the symmetry operations C₂(z), C₃(z), C₄(z), C₅(z) and C₆(z) are obtained easily. The matrices for C_n^m as symmetry operation are calculated by an n-fold multiplication of matrix C_n. The symmetry operation C₂ around axis x (x→x,y→-y, z→-z) and around axis y are (x→-x, y→y, z→-z):

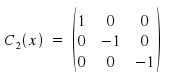
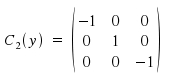
As we know rotatory-reflection to be a combination of rotation and reflection, a matrix representation for this operation is easily to be derived. For instance, to obtain the matrix for rotatory reflection S_n(z) we multiply the matrices for the fundamental operations &sigma_z and C_n.

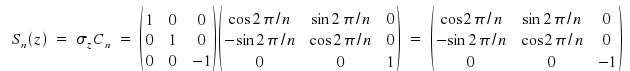
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.