Symmetry Aspects of Electronic Transistions

For atoms, a set of quantum numbers was sufficient to express rules for the selection of electronic transitions. For diatomic molecules, additional symmetry properties had to be introduced: + or − and g or u for homonuclear and + or − for diatomic heteronuclear molecules.

As symmetry is more and more reduced, the quantum numbers in non linear polyatomic molecules become less important. It is only the rule

respective the total spin S which remains important; at least for molecules without atoms of highly charged nuclei, where spin-orbit-interaction occurs. In consequence, the singlet-triplet transitions appear weakly in the spectrum of benzene but quite prominent in the case of iodobenzene.

Whenever electrons change molecular orbitals due to excitation, e.g. in UV spectroscopy, the symmetry of the two involved orbitals is the criterion for a transition. We speak of symmetry-allowed and symmetry-forbidden transitions.

Take the molecular orbitals of trans-butadiene as a first example. Figure 1 is a schematic representation of the energies of these orbitals.

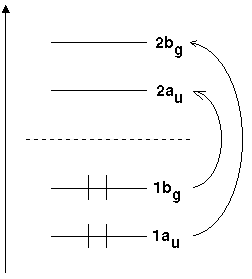Fig 1: Molecular orbitals of butadiene and respective irreducible representations

There is Laporte's rule which states that, for any molecule possessing one centre of inversion, only transitions between g and u or vice versa are allowed.

As the transition dipole moment is a quantum mechanical item which characterizes the intensity of electronic transitions, we expect it to become zero for symmetry-forbidden transitions.

For a start, we confine ourselves to the principles and proceed with simple examples of how the orientation of the transition dipol moment is derived.

For a transition between two electronic states, the selection rules are determined by the symmetry properties of a molecule. In the case of atoms and diatomic molecules, it is as well possible to take symmetry considerations as a base for such rules. But, provided that they are known, it is easier to use the quantum numbers.)

The intensity of an electronic transitions is proportional to the square of the transition dipol moment |R|² and R is:

For an allowed electronic transition |R| ≠ 0. Due to symmetry reasons, we demand for transition dipol moment Γ(ψ) to change the symmetry of the initial state Γ(ψ'') towards the symmetry of the final state Γ(ψ'). The notation Γ(x) represents the symmetry of an object x and accepts values like A₁, A₂ and A₁. In mathematical terms,

• for transitions between non-degenerate states we have
Γ(ψ') x Γ(µ) x Γ(ψ'') =  A
• If at least one of the involved states is degenerate
Γ(ψ') x Γ(µ) x Γ(ψ'') ⊃  A

The symbol ⊃ means "contains" and A represents the total symmetric representation within any point group.

It is possible to resolve the transition dipol moment R into components parallel to the axes of a cartesian coordinate system.

Hence, a transition is allowed if one of the components R_x, R_y or R_z is not equal to zero. The following equations represent the conditions for an allowed transition without involvement of degenerate states of the molecule:

For the presence of one or more degenerate states, the equals sign is replaced by the sign "⊃". T_x, T_y and T_z represent translational components parallel to the cartesian axes.

Whenever the totalsymmetric representation is obtained as the product of two irreducible representations, we are allowed to conclude that two identical representations had been combined. Therefore, an alternative formulation would be

With this set of equations, we have the general rule for transitions between two electronic states. Again, if one or more degenerate states are involved, the equals sign is replaced by "⊃".

In cases where transitions coincide with vibrations of the initial or final state, the electronic transition moment R needs to be replaced by the transition moment R_v.

Here Ψ_v denotes a vibronic wave function. In complete analogy with electronic transitions, we could derive the following set of selection rules for vibronic transistions:

Again, "⊃" replaces the equals sign in cases with one or more degenerate states involved.

Orientation of the transition dipol moment µ

Cs:	Excitation 1A'  ↔1A''. To get from A' to A'' (A' ⊗ ? =  A'') A'' has to be present, i.e. µ has to be perpendicular to the plane of the molecule. (µ within this plane would have symmetry A')
C2v:	Excitation 1A1 ↔ 1B1 (A1 ⊗ ? =  B1). µ needs to have symmetry B2. As B2 corresponds with an orientation along axis y (compare orbital 2py in H2O), µ is situated perpendicular to the molecules plane. Excitation 1B1 ↔1B2 requires µ to have symmetry A2. But there is no transition dipol of this kind, and respectively, this transition is forbidden. The picture changes if we account for vibrational modes too. An asymmtric stretching causes the molecule to get from C2v to Cs and only the molecular plane remains as symmetry element. State B2 becomes A' and state B1 A''. Consequently, the transition dipol moment is of symmetry A'' and perpendicular to the plane of the molecule. Obviously, reduced symmetry increases the number of possible transitions.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.