 |
|---|
 |
|---|
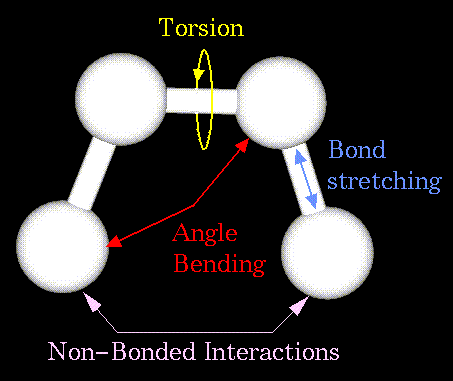
Non-bonded atoms (greater than two bonds apart) interact through van der Waals attraction, steric repulsion, and electrostatic attraction/repulsion. These properties are easiest to describe mathematically when atoms are considered as spheres of characteristic radii.
The object of molecular mechanics is to predict the energy associated with a given conformation of a molecule. However, molecular mechanics energies have no meaning as absolute quantities. Only differences in energy between two or more conformations have meaning. A simple molecular mechanics energy equation is given by:
The mathematical form of the energy terms varies from force-field
to force-field. The more common forms will be described.
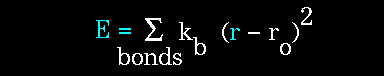 |
|---|
 |
|---|
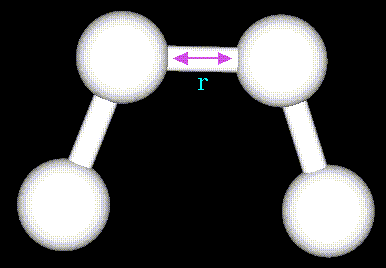
The stretching energy equation is based on Hooke's law. The "kb"
parameter controls the stiffness of the bond spring, while "ro"
defines its equilibrium length. Unique "kb" and "ro" parameters
are assigned to each pair of bonded atoms based on their types (e.g. C-C,
C-H, O-C, etc.). This equation estimates the energy associated with vibration
about the equilibrium bond length. This is the equation of a parabola,
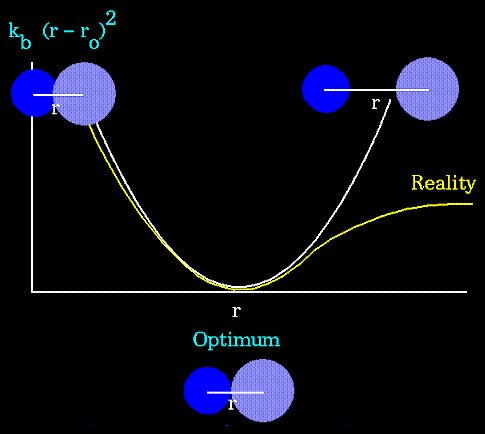
as can be seen in the following plot:
 |
|---|
Notice that the model tends to break down as a bond is stretched toward
the point of dissociation.
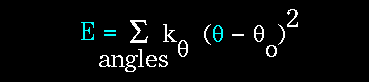 |
|---|
 |
|---|
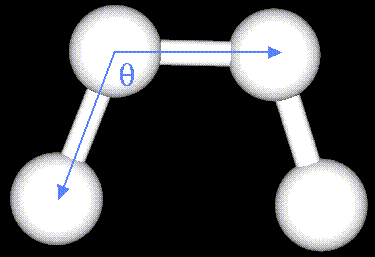
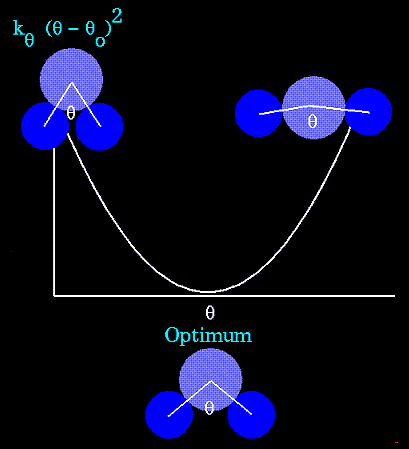
The bending energy equation is also based on Hooke's law. The "ktheta"
parameter controls the stiffness of the angle spring, while "thetao"
defines its equilibrium angle. This equation estimates the energy associated
with vibration about the equilibrium bond angle:
 |
|---|
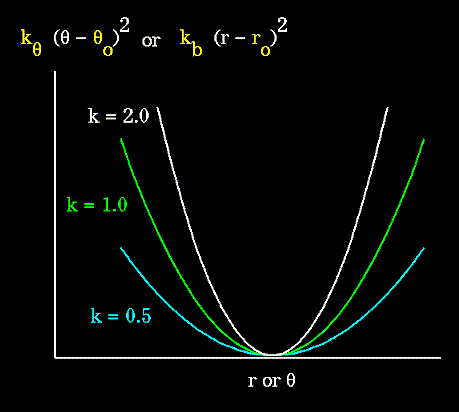
Unique parameters for angle bending are assigned to each bonded triplet
of atoms based on their types (e.g. C-C-C, C-O-C, C-C-H, etc.). The effect
of the "kb" and "ktheta" parameters is to broaden or steepen
the slope of the parabola. The larger the value of "k", the more energy
is required to deform an angle (or bond) from its equilibrium value. Shallow
potentials are achieved for "k" values between 0.0 and 1.0. The Hookeian
potential is shown in the following plot for three values of "k":
 |
|---|
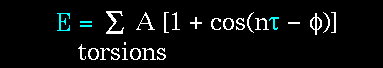 |
|---|
 |
|---|
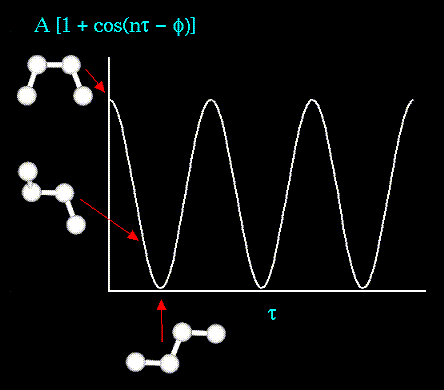
The torsion energy is modeled by a simple periodic function, as can
be seen in the following plot:
 |
|---|
The torsion energy in molecular mechanics is primarily used to correct the remaining energy terms rather than to represent a physical process. The torsional energy represents the amount of energy that must be added to or subtracted from the Stretching Energy + Bending Energy + Non-Bonded Interaction Energy terms to make the total energy agree with experiment or rigorous quantum mechanical calculation for a model dihedral angle (ethane, for example might be used a a model for any H-C-C-H bond).
The "A" parameter controls the amplitude of the curve, the n parameter
controls its periodicity, and "phi" shifts the entire curve along the rotation
angle axis (tau). The parameters are determined from curve fitting. Unique
parameters for torsional rotation are assigned to each bonded quartet of
atoms based on their types (e.g. C-C-C-C, C-O-C-N, H-C-C-H, etc.). Torsion
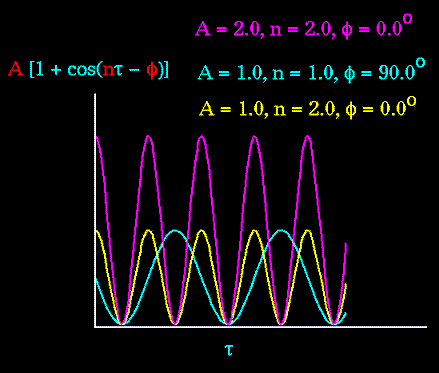
potentials with three combinations of "A", "n", and "phi" are shown in
the following plot:
 |
|---|
Notice that "n" reflects the type symmetry in the dihedral angle. A
CH3-CH3 bond, for example, ought to repeat its energy every 120 degrees.
The cis conformation of a dihedral angle is assumed to be the zero
torsional angle by convention. The parameter phi can be used to synchronize
the torsional potential to the initial rotameric state of the molecule
whose energy is being computed.
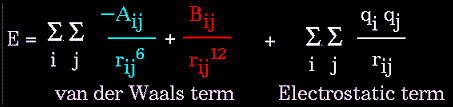 |
|---|
 |
|---|
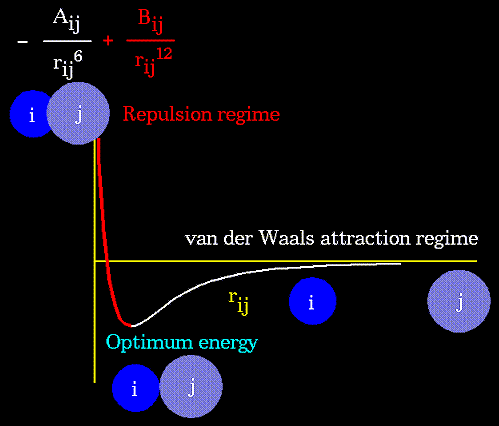
The non-bonded energy accounts for repulsion, van der Waals attraction,
and electrostatic interactions. van der Waals attraction occurs at short
range, and rapidly dies off as the interacting atoms move apart by a few
Angstroms. Repulsion occurs when the distance between interacting atoms
becomes even slightly less than the sum of their contact radii. Repulsion
is modeled by an equation that is designed to rapidly blow up at close
distances (1/r^12 dependency). The energy term that describes attraction/repulsion
provides for a smooth transition between these two regimes. These effects
are often modeled using a 6-12 equation, as shown in the following plot:
 |
|---|
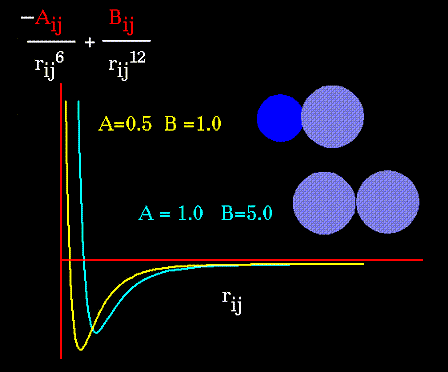
The "A" and "B" parameters control the depth and position (interatomic
distance) of the potential energy well for a given pair of non-bonded interacting
atoms (e.g. C:C, O:C, O:H, etc.). In effect, "A" determines the degree
of "stickiness" of the van der Waals attraction and "B" determines the
degree of "hardness" of the atoms (e.g marshmallow-like, billiard ball-like,
etc.).
 |
|---|
The "A" parameter can be obtained from atomic polarizability measurements, or it can be calculated quantum mechanically. The "B" parameter is typically derived from crystallographic data so as to reproduce observed average contact distances between different kinds of atoms in crystals of various molecules.
The electrostatic contribution is modeled using a Coulombic potential. The electrostatic energy is a function of the charge on the non-bonded atoms, their interatomic distance, and a molecular dielectric expression that accounts for the attenuation of electrostatic interaction by the environment (e.g. solvent or the molecule itself). Often, the molecular dielectric is set to a constant value between 1.0 and 5.0. A linearly varying distance-dependent dielectric (i.e. 1/r) is sometimes used to account for the increase in environmental bulk as the separation distance between interacting atoms increases.
Partial atomic charges can be calculated for small molecules using
an ab initio or semiempirical quantum technique (usually MOPAC or
AMPAC). Some programs assign charges using rules or templates, especially
for macromolecules. In some force-fields, the torsional potential is calibrated
to a particular charge calculation method (rarely made known to the user).
Use of a different method can invalidate the force-field consistency.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.