With the goal of predicting the geometry of a molecule for the ground and possible excited states, A.D. Walsh applied theoretical contributions made by Mulliken. Walsh calculated and discussed the effect of changes in the geometry of a molecule, e.g. a variation of angles, on the energy of molecular orbitals. The so-called Walsh diagrams are an illustration of this dependency. His conclusions are referred to as the rules of Walsh..
 |
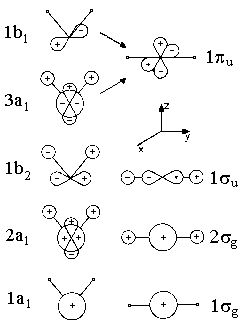 |
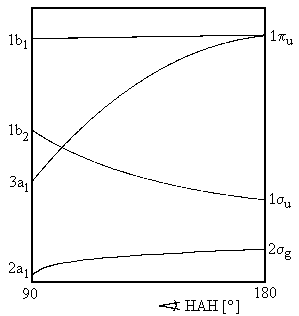
| Fig. 1: Walsh diagram for AH2 | Fig. 2: Schematic representation of the molecular orbitals of AH2 |
Figure 1 displays the energies of orbitals for molecules AH2 as a function of angle HAH. The length of both bonds AH is assumed to be constant and only valence shell electrons are taken into consideration. For the cases of angle HAH = 90° and HAH = 180°, Figure 2 depicts the shapes of these orbitals. The labelling (a1, b2, etc.) is as introduced in chapter on group theory and reflects the orbitals' symmetry properties. For an angle of 180°, i.e. a linear geometry of the molecule, the orbitals are classified with respect to rotational symmetry along the line HAH, i.e. the molecule's axis. The symbols σg, σu, πu etc. refer to the rotational symmetry respective this axis. Within a series of orbitals of one symmetry, numbers are use to specify the orbital lowest energy (e.g. 1b1) and of higher energy (2b1, 3b1, etc.) The following approach is only based on the symmetry species and deals with the consequences of reduced symmetry, e.g. a bending of a linear molecule, for the molecule's orbitals. For example, the degeneracy of molecular energy levels might disappear.
The energetic order of orbitals is dependent on the initial energy of atomic orbitals and the splitting in the LCAO approach, which introduces one bonding orbital of lower and one antibonding orbital of higher energy.
We now ask for the plausible consequences of bending some linear molecule AH2. Orbital πu, which is degenerated for a linear case, splits. We imagine a conversion to one orbital 1b1 with a nodal plane within the plane of H-A-H and another orbital 3a1 with a nodal plane orthogonal to this plane. For the energy of 1b1, which resembles a non-bonding p-orbital, we would not expect a pronounced dependency on the bending angle. In contrast, for 3a1, the zone of overlap increases which, in turn, lowers energy of this state.
The reason for this is (see Figure 2) that a linear conformation does not allow an overlap of the orbitals 2pz of atom A with the orbitals 1s of the Hydrogenium. The more AH2 is bent, the more we recieve are type of bond called a three-center two-electron bonding. On the other hand, the bonding effect of orbital 1σu (thereby becoming an orbital 1b2) is weakened as the linear geometry maximizes the overlap of the central orbital 2py and the atomic orbitals of the hydrogen atoms. Note that the energy of the lowest valence molecular orbital falls.
If the number of valence electrons introduced in a molecule is one or two, these electrons will be found in the orbital 2σg / 2a1. Though not in the erroneous calculations of Walsh's original publication, this orbital falls in energy for angles HAH below 180°. This explains why the molecules with one or two valence shell electrons are bent.
| molecule | angle α |
|---|---|
| H3+ | 60° |
| LiH2+ | 21.1° |
A third electron will occupy orbital 1σu / 1b2 which favours a linear conformation. The influence of this orbital becomes dominant for a four electron system.
| molecule | angle α |
|---|---|
| BeH2+ | 20 ° or 73° |
| BeH2 | 180° |
| BH2+ | 180° |
The data for a molecule BeH2+ need a comment. Like BeH2, the molecule has never been detected in an experiment so far, but there are quite reliable calculations. As shown in Figure 1, the energy lines for the orbital 1b2 and 3a1 intersect somewhere around 90°. This corresponds with two bent structures and two different electronic configurations.
| high angle | (2a1)21b2 | and | 2B2 |
| low angle | (2a1)23a1 | and | 2A1 |
Note that there is a competition between states 2B2 versus 2A1. For each state, there is a hyper potential energy surface (PES) with one minimum. Both surfaces are independent because their symmetry differs. SCF calculations yield the following data for the equilibrium
| state | 2A1 | 2B2 |
|---|---|---|
| angle HBeH | 20° | 73° |
| distance Be-H | 4.43 a0 | 2.63 a0 |
| distance H-H | 1.52 a0 | 3.14 a0 |
The state 2B2 is an example of an three-electron two-center bonding. An equilateral triangle describes the molecule roughly. Although the energy of the molecule is about 150 kJ/mol above the energy of Be+ (1s22s) and H2 it is stable against dissociation (bonding energy approximately 290 kJ/mol). It seems that 2B2 represents a state of BeH2 where bonding energy is below the promotion energy needed to lift Be+ from the ground state towards the valence state. Nevertheless, it is this state that fits into the series of molecules AH2 we apply the rules of Walsh. As suggested by ?*seiner equilibrium theory?*, the ground state 2A1 would rather be described as a complex between Be+ and H2 than as a molecule BeH2+.
In accordance with Walsh's rules, the uncharged molecule BeH2 is linear in its ground state and 2.53 a0 are found as distance Be-H. The electronic configuration is 1σg2 2σg2 1σu2. A number of four instead of three electrons in bonding molecular orbitals (2σg and 1σu) stabilizes the molecule and in fact the energy of this molecule is about 630 kJ/mol below the Be + 2H and even approximately 170 kJ/mol below Be + H2 in their ground state. Nevertheless, BeH2 has never been detected, but this is due to the ability of the molecule to compensate some electron deficiency via hydrogen bonds which introduce polymerization of the compound.
BeH2 and the isoelectronic BH2+ have four valence electrons. In molecules with five or six valence electrons, e.g. BH2 or CH2, Walsh's diagramm suggests that orbital 3a1 harbours the additional electrons. This orbital would favour an bent conformation. In fact, all molecules with five or six valence electrons are angular.
| molecule | angle α |
|---|---|
| BH2 | 131° |
| CH2 (Singlet) | 102° |
| CH2 (Triplet) | 136° |
A seventh and eighth electron will be found in orbital 1b1. As there is no dependency between this orbital's energy and the angle HAH, the molecules of this group are bent as well.
| molecule | angle α |
|---|---|
| NH2 | 103.4° |
| OH2 | 104.5° |
The molecule CH2 is a special case. In the linear conformation, the 1πu energy level is only doubly occupied but could harbour four electrons. The molecule represents an open shell configuration which, like the ground state of O2, consists of several terms, i.e. 3σg−, 1Δg, 1σg+. Following the rule of Hund, the triplet 3σg− is the lowest in energy. If we bend the molecule, the terms change: 3σg− shifts to 3B1, 1Δg splits in the two terms 1A1 and 1B1, whereas 1σg+ becomes 1A1. For a molecule with 180° we certainly have, in accordance with Hund's rule the lowest energy for 3B1. As long as the splitting due to interaction of electrons exceeds the splitting of the 1πu level introduced by bending and some lower symmetry, we may approach the problem in this way. In contrast, for small angles, where the separation between the energies of 3a1 and 1b1 becomes larger than the energy due the term splitting, another approach is needed. In such cases, the building-up principle is the first to be considered: Six electrons are to be distributed among the orbitals 2a1, 1b2 and 3a1. As all shells are completely filled, a totalsymmetric state, i.e. a 1A1-term is reached.
Whether the real ground state molecule CH2 is characterized by the term 3B1 (with some angle HAH representing the lowest energy) or by the term 1A1 (with some other angle HAH) remains open in our qualitative treatment of the molecule. Both states only differ by a small amount of energy. This energy appears in Figure 3. The energy curves shown there result from ab initio calculations and suggest that 3B1 is the ground state of CH2.
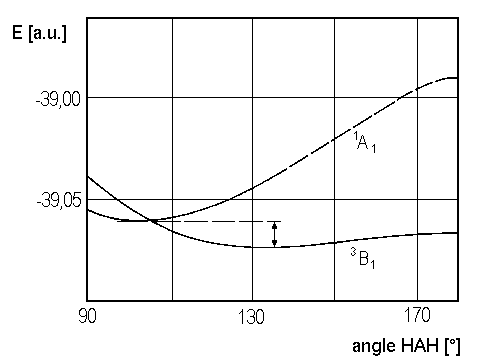 |
| Fig. 3: Potential curves of the lowest of CH2, according to V. Staemmler [Theoret. Chim. Acta 31, 49 (1973)] |
But, anyway, Walsh's diagram leads to the conclusion, that state 3B1 with the open shell configuration 2a12, 1b22 3a1 1b1 favours a greater equilibrium angle (close to 180°) than state 1A1 with 2a12 1b22 3a12 as electronic configuration.
The table below summarizes Walsh's rules for molecules AH2 in their ground states.
| Number of valence electrons |
Geometry of molecule AH2 |
|---|---|
| 1 &minus 3 | bent |
| 4 | linear |
| 5 | weakly bent |
| 6 − 8 | bent |
| 9 | weakly bent |
| 10 &minus 12 | linear |
Cases with 9 to 12 valence electrons are only discussed among theoreticians as there a no respective molecules in nature. A hypothetic NeH2 would have 10 valence electrons.
Table 1: Examples for electronic configurations and the geometry predicted by the Walsh diagram.
| Valence electrons | Molecule | angle HAH | linear, D∞h | angular, C2v |
|---|---|---|---|---|
| 2 | LiH2+ | 21.1° | 1σg: 2σg2 | 1A1: 2a12 |
| 3 | BeH2+ | 73° | 2σu: 2σg2 1σu | 2B2: 2a12 1b2 |
| 4 | BeH2 | 180° | 2σg: 2σg2 1σu2 | 1A1: 2a12 1b22 |
| BH2+ | 180° | 2σg: 2σg21σu2 | 1A1: 2a12 1b22 | |
| 5 | BH2 | 131° | 2Πu:1σu2 1πu | 1A1: 1b22 3a1 |
| 6 | 3CH2 | 136° | 3Σ: 1σu2 1πu2 | 3B1: 1b223a1 1b1 |
| 1CH2 | 102° | 1Σ,1Δ:1σu2 1pu2 | 1A1: 1b22 3a12 | |
| 7 | NH2 | 103.4° | 2Πu:1σu2 1πu3 | 2B1: 3a121b1 |
| 8 | OH2 | 104.5° | 1σg: 1σu1 1πu4 | 1A1: 3a12 1b12 |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.