 |
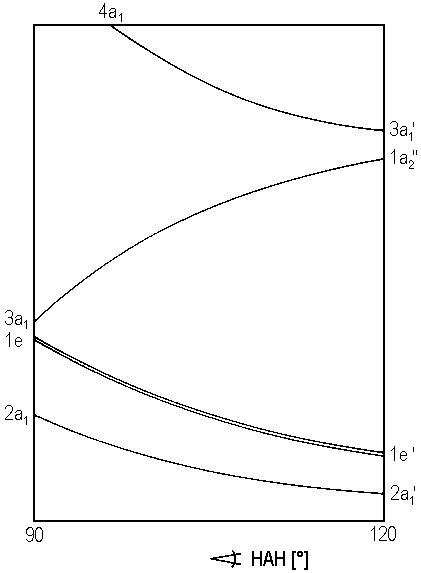
| Fig. 1: Walsh's diagram for molecules AH3 |
In one of the previous chapters, the conformation of a molecule AH2 was predicted with reference to Walsh's diagram which shows how the energies of orbitals vary with angle HAH. Provided that symmetry C3v is maintained, an analogous approach is possible for molecules AH3. The respective Walsh diagram is shown as Figure 1. Note that an angle HAH of 120° indicates planar geometry and a case of symmetry D3h, whereas angles below 120° represents a pyramidal geometry and symmetry C3v.
For a number of valence shell electrons between 1 and 14, the table below shows the results for the geometry of AH3 in the ground state of the molecule.
| Valence electrons | Geometry |
|---|---|
| 1 - 4 | planar |
| 5 - 6 | planar |
| 7 - 9 | pyramidal |
| 10 - 14 | planar |
The are hardly any known instances of molecules AH3 with 1 - 4 valence electrons. Quantum chemistry theoreticians focussed on BeH3+ which has four valence electrons. Obviously, this cationic molecule is planar in its ground state. But, instead of falling in point group D3h it has symmetry C2v. Figure 2 illustrates the assumed molecular structure. The molecule can be regarded as a loose complex between BeH+ and hydrogen H2.
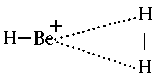 |
| Suggested structure for the cationic molecule BeH3+ |
Further examples of AH3
Although Walsh's rules appear simple, a reliable calculation of the geometry of a molecule AH3 based on quantum chemistry costs high efforts. Another goal besides the equilibrium geometry of such a molecule is the difference between the equilibrium energy and the lowest energy for a planar state of the molecule, i.e. the so-called inversion barrier EI. This energy is decisive for a relative change of the four atoms's position. Starting with pyramidal conformation and with a transitional state characterized by all four atoms A and H lying within one plane, inversion leaves the hydrogen atoms in positions beyond this plane. Finally, the three atoms H and A form a pyramidal molecule.
The probability for such an inversion is dependent on the average thermal energy of molecules and the inversion barrier. Therefore, the frequency of such inversions is dependent on temperature.
Attempts to calculate equilibrium geometries and inversion barriers for molecules AH3 by use of the SCF method with linearily combined atomic orbitals yield no satisfying results. These results are improved by introducing a so-called polarization function to the basis set, i.e. d-type wave functions for atom A and p-type wave functions for the hydrogen atoms. In the case of ammonia, an approach without polarization function predicts α = 120°, i.e. the molecule would prefer a planar structure as this is lower in energy. In contrast, an SCF calculation with such a function yields α = 107° and EI = 22 kJ/mol, which is in good accordance with experimental data α = 106°7' and EI = 24 kJ/mol. Thus, the use of polarization functions corrects some bias towards a planar conformation and erroneous low values for the inversion barrier.
It is striking that the molecules CH3− and OH3+ isoelectronic to ammonia differ remarkably with respect to equilibrium conformation and inversion barrier. For both ionic molecules, this energy is in the order of 4 kJ/mol. Note that for PH3 an inversion barrier of 150 kJ/mol has been determined.
If we want to apply Walsh's concept to molecules AH4, the situation gets even more complicated as five parameters are necessary to describe their geometry. With AH2, we had only one angle and with AH3 three angles as degrees of freedom. In consequence, for AH4, a Walsh diagram in six dimensions had to be considered, which is an approach not too beneficial.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.