



Next: The Intensity of Spectral
Up: Optical Transitions and Spectral
Previous: Optical Transitions and Spectral
Contents
In emission spectroscopy a molecule undergoes a
transition from a high energy state 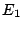 to a state of lower energy
to a state of lower energy 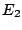 and emits the excess
energy as a photon. In absorption spectroscopy the absorption of nearly monochromatic
incident radiation is monitored as function of the radiation frequency. Anyway, the energy of
the emitted, or absorbed photon
and emits the excess
energy as a photon. In absorption spectroscopy the absorption of nearly monochromatic
incident radiation is monitored as function of the radiation frequency. Anyway, the energy of
the emitted, or absorbed photon 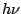 is given by the Bohr formula
is given by the Bohr formula
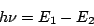 |
(6) |
These are two convenient units which are often used by spectroscopists for characterizing a
transition energy:
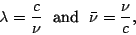 |
(7) |
where the wavelength 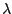 is measured in nanometers, microns, or Ångströms
(1 Å= 0,1 nm) and the units of wavenumber
is measured in nanometers, microns, or Ångströms
(1 Å= 0,1 nm) and the units of wavenumber 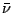 are almost always chosen as reciprocal centimeters (
are almost always chosen as reciprocal centimeters (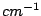 ). It is easy to see that
). It is easy to see that
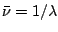 .
.
Emission and absorption spectroscopy give the same information about energy level separation and only practical considerations generally determine which technique is employed.
As known from the Einstein theory of radiation spontaneous decay of the excited state 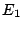 can
be described by the equation
can
be described by the equation
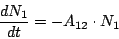 |
(8) |
where 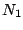 is population of the level
is population of the level 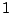 and
and 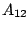 is the Einstein coefficient of
spontaneous emission.
is the Einstein coefficient of
spontaneous emission.
This equation has the evident solution
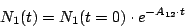 |
(9) |
The life time 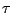 of the state is defined as the time needed for a reduction of the
level population by a factor of 1/e. Thus,
of the state is defined as the time needed for a reduction of the
level population by a factor of 1/e. Thus,
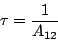 |
(10) |
If the molecule is initially in its lower state 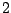 interacting with incident radiation the
transition rate of the stimulated absorption from the state
interacting with incident radiation the
transition rate of the stimulated absorption from the state 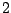 to the state
to the state 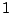 is
is
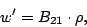 |
(11) |
where 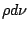 is the radiation energy density and
is the radiation energy density and 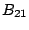 is the Einstein coefficient of
stimulated absorption.
is the Einstein coefficient of
stimulated absorption.
If the molecule is initially in its upper state 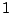 interacting with incident radiation
population of the state
interacting with incident radiation
population of the state 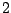 through stimulated emission transition obeys the equation
through stimulated emission transition obeys the equation
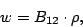 |
(12) |
where 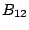 is the Einstein coefficient of stimulated emission.
is the Einstein coefficient of stimulated emission.
Relationship between all three Einstein coefficients is as follows
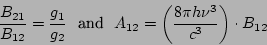 |
(13) |
where 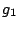 and
and 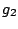 are the multiplicities of degeneracy of the corresponding states. If the
degeneracy of both states is the same, we have
are the multiplicities of degeneracy of the corresponding states. If the
degeneracy of both states is the same, we have
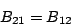 |
(14) |




Next: The Intensity of Spectral
Up: Optical Transitions and Spectral
Previous: Optical Transitions and Spectral
Contents
Markus Hiereth
2005-01-20
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() can
be described by the equation
can
be described by the equation
![]() of the state is defined as the time needed for a reduction of the
level population by a factor of 1/e. Thus,
of the state is defined as the time needed for a reduction of the
level population by a factor of 1/e. Thus,
![]() interacting with incident radiation the
transition rate of the stimulated absorption from the state
interacting with incident radiation the
transition rate of the stimulated absorption from the state ![]() to the state
to the state ![]() is
is
![]() interacting with incident radiation
population of the state
interacting with incident radiation
population of the state ![]() through stimulated emission transition obeys the equation
through stimulated emission transition obeys the equation