



Next: Symmetry of Vibration and
Up: Symmetry of Normal Vibrations
Previous: Effect of Symmetry Operations
Contents
Let us consider the normal vibrations of a linear triatomic molecule, like 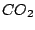 . The two
vibrations
. The two
vibrations 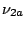 and
and 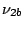 are obviously degenerate with each other. They are
antisymmetric with respect to an inversion at a center of symmetry as is the
vibration
are obviously degenerate with each other. They are
antisymmetric with respect to an inversion at a center of symmetry as is the
vibration 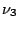 . Another possible symmetry operation is rotation
. Another possible symmetry operation is rotation
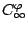 by an
arbitrary angle
by an
arbitrary angle 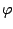 about the internuclear axis. This rotation leaves the vibrations
about the internuclear axis. This rotation leaves the vibrations
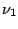 and
and 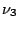 unchanged, however, both
unchanged, however, both 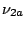 and
and 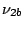 are changes by more than
just a sign. In other words, the vibrations
are changes by more than
just a sign. In other words, the vibrations 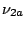 and
and 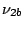 are neither
symmetric, nor antisymmetric with respect to the rotation
are neither
symmetric, nor antisymmetric with respect to the rotation
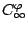 . The
displacement normal coordinates after the rotation
. The
displacement normal coordinates after the rotation 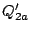 ,
, 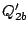 can be
expressed over the normal coordinates before the rotation
can be
expressed over the normal coordinates before the rotation 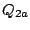 ,
, 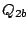 as
as
Therefore, degenerate vibrations, in general, transformed under a symmetry operation as
a linear combination of each other. This result is valid for any number of the degenerate
vibrations and any type of symmetry operations involved.




Next: Symmetry of Vibration and
Up: Symmetry of Normal Vibrations
Previous: Effect of Symmetry Operations
Contents
Markus Hiereth
2005-02-09
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.