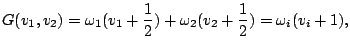 |
(15) |
The corresponding total vibrational eigenfunction can be written as (see
eq. (14))
If ![]() , than
, than
![]() and there is only one function
and there is only one function
![]() in eq. (16). Thus, the zero-point vibrational
in eq. (16). Thus, the zero-point vibrational ![]() does not
introduce a degeneracy. In this case, the same relations apply as in the previous section.
does not
introduce a degeneracy. In this case, the same relations apply as in the previous section.
If the degenerate vibration if excited by only one quantum, we have either ![]() , or
, or
![]() for which the wavefunctions
for which the wavefunctions ![]() in eq. (16) are not the same.
That is, there are two eigenfunctions for the state
in eq. (16) are not the same.
That is, there are two eigenfunctions for the state ![]() with the energy
with the energy
![]() , see eq. (15). Therefore, the state
, see eq. (15). Therefore, the state ![]() is doubly degenerate. Note, that
any linear combination of the two wavefunctions in eq. (16) is also an eigenfunction
of the same energy level.
is doubly degenerate. Note, that
any linear combination of the two wavefunctions in eq. (16) is also an eigenfunction
of the same energy level.
If two quanta are excited (![]() ), we may have either
), we may have either ![]() , or
, or ![]() , or
, or
![]() , that is there is a triple degeneracy. In general, the degree of degeneracy if
, that is there is a triple degeneracy. In general, the degree of degeneracy if
![]() quanta of the double degenerate vibration are excited, is equal to
quanta of the double degenerate vibration are excited, is equal to ![]() .
.
Important result: Total vibrational eigenfunctions, corresponding to a degenerate
vibration are neither symmetric, nor antisymmetric, but can in general be transformed under a
symmetry operation as a linear combination of each other. However, there is only one zero-point
![]() vibration wavefunction
vibration wavefunction ![]() which must be either symmetric, or antisymmetric
under a symmetry operation.
which must be either symmetric, or antisymmetric
under a symmetry operation.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.