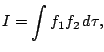 |
(25) |
Let us consider the overlap integral
The integral ![]() is always a scalar value which means that it does not changes under
any symmetry transformations of the molecule. The volume element
is always a scalar value which means that it does not changes under
any symmetry transformations of the molecule. The volume element ![]() is also a scalar as it
is invariant under any coordinate transformations. Therefore, the product
is also a scalar as it
is invariant under any coordinate transformations. Therefore, the product ![]() must also
remain unchanged by any symmetry operations of the molecular point group. If
the integrand changes its sign under a symmetry operation, the integral
must also
remain unchanged by any symmetry operations of the molecular point group. If
the integrand changes its sign under a symmetry operation, the integral ![]() is necessary zero,
because its positive part will necessary cancel its positive part. As we know, the the
irreducible representation which is equivalent in the molecular point group is
totally symmetric representation
is necessary zero,
because its positive part will necessary cancel its positive part. As we know, the the
irreducible representation which is equivalent in the molecular point group is
totally symmetric representation ![]() . Thus, the integral
. Thus, the integral ![]() differs from zero only
if the integrand
differs from zero only
if the integrand ![]() spans the symmetry species
spans the symmetry species ![]() .
.
If the symmetry species of the functions ![]() and
and ![]() are known, the group theory provides a
formal procedure which can be used for determination of the symmetry species of the product
are known, the group theory provides a
formal procedure which can be used for determination of the symmetry species of the product ![]() . Particularly, the character table of the product
. Particularly, the character table of the product ![]() can be obtained just by
multiplication of the characters from the character tables of the functions
can be obtained just by
multiplication of the characters from the character tables of the functions ![]() and
and
![]() corresponding to a certain symmetry operator.
corresponding to a certain symmetry operator.
As an example we consider the product of the ![]() orbital of the
orbital of the ![]() atom and the linear
combination of three hydrogen atom orbitals,
atom and the linear
combination of three hydrogen atom orbitals, ![]() in eq. (20) in
in eq. (20) in ![]() molecule, each of the orbitals spans
molecule, each of the orbitals spans ![]() species:
species:
It is evident from eq. (26) and the table 5 , that the product ![]() also spans
also spans ![]() and therefore, the in integral
and therefore, the in integral ![]() in eq. (25) in this case is
not necessary equal to zero. Therefore, bonding and antibonding molecular orbitals
can be formed from linear combinations of
in eq. (25) in this case is
not necessary equal to zero. Therefore, bonding and antibonding molecular orbitals
can be formed from linear combinations of ![]() and
and ![]() .
.
The procedure of finding the irreducible representation of the product of two representations
![]() and
and ![]() is written as direct product of irreducible representations
is written as direct product of irreducible representations
![]() and and for the example above can be written as
and and for the example above can be written as
![]() .
.
As another example, we consider the product of the ![]() orbital of the
orbital of the ![]() atom in
atom in ![]() and
and ![]() , where
, where ![]() is the linear combination of the hydrogen atom
wavefunctions from eq. (21). Now one function spans the
is the linear combination of the hydrogen atom
wavefunctions from eq. (21). Now one function spans the ![]() species and another the E
species. The product table of characters is
species and another the E
species. The product table of characters is
The product characters 2, ![]() , 0 are those of the E species alone and therefore, the integral
must be zero. Therefore, bonding and antibonding molecular orbitals cannot be formed
from linear combinations of
, 0 are those of the E species alone and therefore, the integral
must be zero. Therefore, bonding and antibonding molecular orbitals cannot be formed
from linear combinations of ![]() and
and ![]() . The direct product of the representations in this
case is written as
. The direct product of the representations in this
case is written as ![]() E
E![]() E.
E.
The general rule is that only orbitals of the same symmetry species may have nonzero
overlap and therefore, form bonding and antibonding combinations. This result makes a
direct link between the group theory and construction of molecular orbitals from atomic orbitals
by the LCAO procedure we discussed in previous chapter. Indeed, the molecular orbitals can be
formed only from a particular set of atomic orbitals with nonzero overlap. These molecular
orbitals are usually labelled with a lower-case letter corresponding to the symmetry species.
For instance, the (![]() ) molecular orbitals are called
) molecular orbitals are called ![]() if they are bonding and
if they are bonding and
![]() if they are antibonding.
if they are antibonding.
Note, that the relationship between the symmetry species of the atomic orbitals and their
product, in general, is not as simple as in eqs. (26) and (27). As an example,
let us consider the linear combinations ![]() and
and ![]() in eq. (21) which both have
symmetry species E. As we know the
in eq. (21) which both have
symmetry species E. As we know the ![]() atomic orbital cannot be used together with each of
them for building the bonding and antibonding molecular orbitals. However, the
atomic orbital cannot be used together with each of
them for building the bonding and antibonding molecular orbitals. However, the ![]() and
and
![]() atomic orbitals also belong to the E species in
atomic orbitals also belong to the E species in ![]() (see Character
Table 5) and thus are suitable because they may have a nonzero overlap with
(see Character
Table 5) and thus are suitable because they may have a nonzero overlap with ![]() and
and ![]() . This construction can be verified by multiplying the characters as
. This construction can be verified by multiplying the characters as
It can be easily verified from eq. (28) by making summation of characters in
Table 5 that E ![]() E
E
![]() E. The product
E. The product ![]() in
eq. (28) contains the totally symmetric species
in
eq. (28) contains the totally symmetric species ![]() and, therefore, the corresponding
integral may have a nonzero value.
and, therefore, the corresponding
integral may have a nonzero value.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.