



Next: Group Multiplication Table
Up: The Symmetry Classification of
Previous: Definition of the Group
Contents
Particularly we will consider the following point groups which molecules can belong to.
- 1. The groups
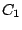 ,
, 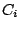 , and
, and 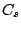 .
.
- A molecule belongs to the group
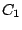 if it has no
elements other than identity
if it has no
elements other than identity 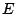 . Example: DNA. A molecule belongs to the group
. Example: DNA. A molecule belongs to the group 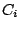 , if it
consist of two operations: the identity
, if it
consist of two operations: the identity 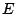 and the inversion
and the inversion 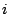 . Example: meso-tartaric
acid. A molecule belongs to the group
. Example: meso-tartaric
acid. A molecule belongs to the group 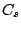 ,
if it consists of two elements: identity
,
if it consists of two elements: identity 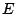 and a mirror plane
and a mirror plane 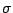 . Example:
. Example: 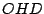 .
.
- 2. The group
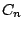 .
.
- A molecule belongs to the group
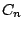 if it has a n-fold axis.
Example:
if it has a n-fold axis.
Example: 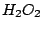 molecule belongs to the
molecule belongs to the 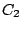 group as it has the elements
group as it has the elements 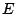 and
and 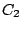 .
.
- 3. The group
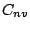 .
.
- A molecule belongs to the group
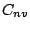 if in addition to the
identity
if in addition to the
identity 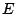 and a
and a 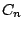 axis, it has
axis, it has 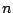 vertical mirror planes
vertical mirror planes 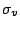 . Examples:
. Examples: 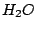 molecule belongs to the
molecule belongs to the 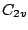 group as it has the symmetry elements
group as it has the symmetry elements 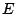 ,
, 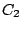 , and two
vertical mirror planes which are called
, and two
vertical mirror planes which are called 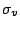 and
and 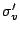 . The
. The 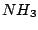 molecule
belongs to the
molecule
belongs to the 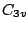 group as it has the symmetry elements
group as it has the symmetry elements 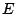 ,
, 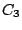 , and three
, and three
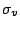 planes. All heteroatomic diatomic molecules and
planes. All heteroatomic diatomic molecules and 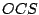 belong to the group
belong to the group
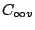 because all rotations around the internuclear axis and all reflections
across the axis are symmetry operations.
because all rotations around the internuclear axis and all reflections
across the axis are symmetry operations.
- 4. The group
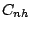 .
.
- A molecule belongs to the group
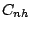 if in addition to the
identity
if in addition to the
identity 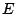 and a
and a 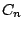 axis, it has a horizontal mirror plane
axis, it has a horizontal mirror plane 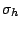 . Example:
butadiene
. Example:
butadiene 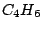 , which belongs to the
, which belongs to the 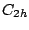 group, while
group, while 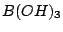 molecule belongs to
the
molecule belongs to
the 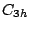 group. Note, that presence of
group. Note, that presence of 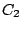 and
and 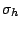 operations imply the presence
of a center of inversion. Thus, the group
operations imply the presence
of a center of inversion. Thus, the group 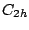 consists of a
consists of a 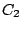 axis, a horizontal
mirror plane
axis, a horizontal
mirror plane 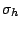 , and the inversion
, and the inversion 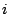 .
.
- 5. The group
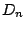 .
.
- A molecule belongs to the group
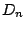 if it has a n-fold
principal axis
if it has a n-fold
principal axis 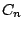 and
and 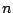 two-fold axes perpendicular to
two-fold axes perpendicular to 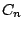 .
. 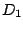 is of cause
equivalent with
is of cause
equivalent with 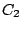 and the molecules of this symmetry group are usually classified as
and the molecules of this symmetry group are usually classified as
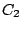 .
.
- 6. The group
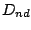 .
.
- A molecule belongs to the group
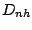 if in addition to the
if in addition to the
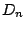 operations it possess
operations it possess 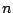 dihedral mirror planes
dihedral mirror planes 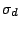 . Example: The twisted,
. Example: The twisted,
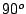 allene belongs to
allene belongs to 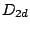 group while the staggered confirmation of ethane belongs
to
group while the staggered confirmation of ethane belongs
to 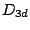 group.
group.
- 7. The group
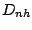 .
.
- A molecule belongs to the group
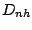 if in addition to the
if in addition to the
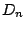 operations it possess a horizontal mirror plane
operations it possess a horizontal mirror plane 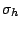 . As a
consequence, in the presence of these symmetry elements the molecule has also necessarily
. As a
consequence, in the presence of these symmetry elements the molecule has also necessarily
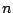 vertical planes of symmetry
vertical planes of symmetry 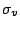 at angles 360
at angles 360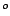 /2
/2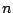 to one another.
Examples:
to one another.
Examples: 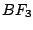 has the
elements
has the
elements 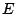 ,
, 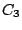 ,
, 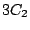 , and
, and 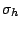 and thus belongs to the
and thus belongs to the 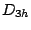 group.
group. 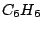 has the elements
has the elements 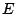 ,
, 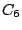 ,
, 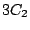 ,
, 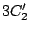 and
and 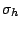 and thus belongs to the
and thus belongs to the 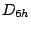 group. All homonuclear diatomic molecules, such as
group. All homonuclear diatomic molecules, such as 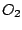 ,
, 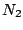 , and others belong to the
, and others belong to the
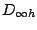 group. Another examples are ethene
group. Another examples are ethene 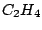 (
(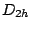 ),
), 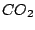 (
(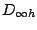 ),
), 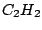 (
(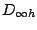 ).
).
- 8. The group
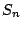 .
.
- A molecule belongs to the group
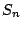 if it possess one
if it possess one
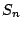 axis. Example: tetraphenylmethane which belongs to the group
axis. Example: tetraphenylmethane which belongs to the group 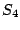 . Note, that the
group
. Note, that the
group 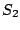 is the same as
is the same as 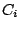 , so such molecules have been classified before as
, so such molecules have been classified before as 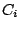 .
.
- 9. The cubic groups.
- There are many important molecules with more than one principal
axes, for instance,
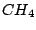 and
and 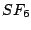 . Most of them belong to the cubic groups, particularly
to tetrahedral groups
. Most of them belong to the cubic groups, particularly
to tetrahedral groups 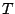 ,
, 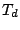 , and
, and 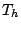 , or to the octahedral groups
, or to the octahedral groups
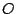 and
and 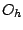 . If the object has the rotational symmetry of the tetrahedron, or octahedron,
but has no their planes of reflection, then it belongs to the simpler groups
. If the object has the rotational symmetry of the tetrahedron, or octahedron,
but has no their planes of reflection, then it belongs to the simpler groups 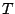 , or
, or 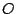 .
The group
.
The group 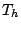 is based on
is based on 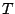 , but also has a center of inversion.
, but also has a center of inversion.
- 10. The full rotational group
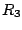 .
.
- This group consists of infinite number of
rotational axes with all possible values of
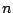 . It is the symmetry of a sphere. All atoms
belong to this symmetry group.
. It is the symmetry of a sphere. All atoms
belong to this symmetry group.




Next: Group Multiplication Table
Up: The Symmetry Classification of
Previous: Definition of the Group
Contents
Markus Hiereth
2005-02-09
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.