Maxwellsche Beziehungen
Wir haben jetzt vier thermodynamische Funktionen kennen gelernt, die eine
Energie darstellen: U, H, A und G. Diese Funktionen wollen
wir zunächst etwas näher betrachten und einige wichtige Beziehungen
ableiten, wobei wir uns auf geschlossene Systeme beschränken wollen,
bei denen reine homogene Stoffe vorliegen und Arbeit ausschließlich
als Volumenarbeit auftreten möge.
Für die Innere Energie gilt nach dem Ersten Hauptsatz:
Ersetzen wir dqrev durch den Entropieterm Tds und dwrev durch die reversible Volumenarbeit -pdV, do erhalten wir
Da die Enthalpie H = U + pV ist, dH = dU + pdV + Vdp, folgt
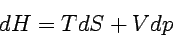 |
Nach der Definition für die Freie Energie, A = U - TS, muss dA = dU - TdS + SdT sein, mit dU = TdS - pdV also
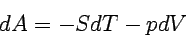 |
Entsprechend für die Freie Enthalpie:
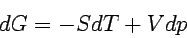 |
Die vier unterlegten Gleichungen nennt man die charakteristischen Funktionen.
Mit Hilfe eines Merkschemas, das auf Guggenheim zurückzuführen ist, können wir uns diese (und noch später folgende) Beziehungen leicht merken:
| S | U | V | ||
| + | H | A | − | |
| p | G | T |
Jede der vier abhängigen Variablen (U,H,A,G) ist von den beiden zugehörigen unabhängigen umgeben, von denen die in der linken Spalte stehenden mit positivem, die in der rechten stehenden mit neagtiven Vorzeichen auftreten. Die Produkte auf der rechten Seite der charakteristischen Funktionen bestehen jeweils aus einer extensiven (S und V) und einer intensiven (p und T) Zustandsgröße, die im Merkschema einander gegenüber angeordnet sind.
Den charakteristischen Funktionen kommt eine zentrale Bedeutung zu, denn mit ihrer Hilfe können wir alle thermodynamischen Funktionen durch eine charakteristische Funktion und ihre Ableitung nach geeigneten Variablen ausdrücken. Die insgesamt 33 zwischen den thermodynamischen Größen U, H, A, G, T, S, p und V bestehenden ersten partiellen Differentialquotienten können wir leicht ineinander umrechnen, um so experimentell nicht oder nur schwierig zu bestimmende Größen auf leicht zugängliche Größen wie cp, α, κ oder dergleichen zurückzuführen.
Da die charakteristischen Funktionen totale Differentiale sind, stellen
die in diese Gleichungen auftretenden Größen T, p, S und V gleichzeitig
partielle Differentialquotienten dar. Als Beispiel betrachten wir das totale
Differential der Inneren Energie U(S,V):
Wenn wir U als Funktion von S und V behandeln, dann lässt
sich - als mathematisches Konsequenz daraus - die Änderung dU in Abhängigkeit
von dS und dV ausdrücken:
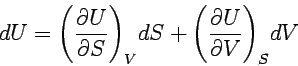
Vergleicht man diesen Ausdruck mit der thermodynamischen Gleichung, dU = TdS - pdV, so ergibt sich
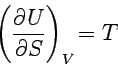 und
und
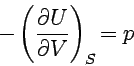
Die erste Gleichung ist eine rein thermodynamische Definition der Temperatur als Verhältnis der Änderung von Innerer Energie und Entropie in einem geschlossenen System bei konstantem Volumen. Entsprechend verfahren wir mit den anderen charakteristischen Funktionen und erhalten so:
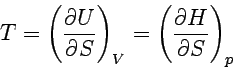 |
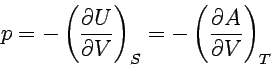 |
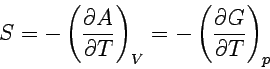 |
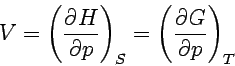 |
Auch diese Beziehungen folgen aus dem Guggenheimschen Merkschema. Die an einer Ecke des Schemas stehende Funktion ergibt sich als partielle Ableitung der ihr im Schema gegenüberstehenden Energiefunktion (z.B. bei T die Funktionen U und H) nach der ihr diagonal gegenüberstehenden thermodynamischen Größe (im Beispiel S). Die Beziehungen sind in zweierlei Weise wichtig: Einmal ergeben sie Beziehungen zwischen den verschiedenen partiellen Differentialquotienten, zum anderen liefern sie Angaben zu so bedeutenden Fragen wie der Temperatur- oder Druckabhängigkeit der Freien Enthalpie, die wir später immer wieder benötigen werden.
Weitere Beziehungen, die sogenannten Maxwellschen Beziehungen, gewinnen wir, wenn wir berücksichtigen, dass die aus den obigen Gleichungen berechenbaren gemischten zweiten partiellen Differentialquotienten einander gleich sein müssen. So ist bespielsweise die gemischte 2. Ableitung von U nach S und V nach der ersten Gleichung ∂2U/∂S∂V = ∂(∂U/∂S)/∂V = (∂T/∂V)S, nach der zweiten aber ∂2U/∂V∂S = ∂(∂U/∂V)/∂S = − (∂p/∂S)V.
| Maxwellsche Beziehungen | 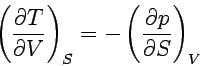 |
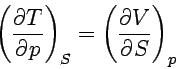 | |
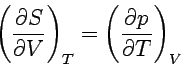 | |
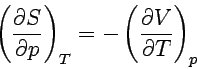 |
Man kann mit Hilfe der Maxwellschen Beziehungen sehr einfache Abhängigkeiten berechnen. Ein Beispiel ist die Druckabhängigkeit der Entropie: Aus der letzten Gleichung folgt:
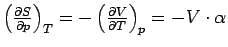
wobei auch gleichzeitig die schwer meßbare Größe auf
eine experimentell leicht zugängliche zurückgeführt ist.
Aus den charakteristischen Funktionen folgt sofort:
| 1. Freie Energie | Temperaturabhängigkeit | 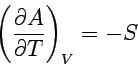 |
| Volumenabhängigkeit | 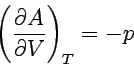 |
|
| 2. Freie Enthalpie | Temperaturabhängigkeit | 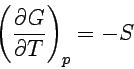 |
| Druckabhängigkeit | 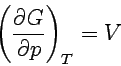 |
|
| 3. Entropie | Temperaturabhängigkeit | 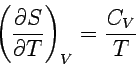 |
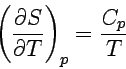 |
Wir können nun leicht Abhängigkeiten der Freien Enthalpie von Druck und Temperatur ableiten.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.