Die Entropie eines Systems bei der Temperatur T kann auf seine Entropie bei T = 0 K zurückgeführt werden, indem man die Wärmekapazität Cp bei verschiedenen Temperaturen misst und mit Hilfe dieser Daten das Integral ∫(CpT-1)dT auswertet. Dabei muss man für jeden Phasenübergang zwischen T = 0 und der betrachteten Temperatur die jeweilige Phasenübergangsentropie (ΔtH/Tt) addieren. Wenn eine Substanz bei TSm schmilzt und bei TS siedet, dann ist ihre Entropie oberhalb der Siedetemperatur:
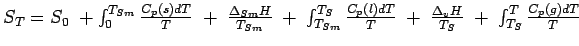
Mit Ausnahme von S(0) können alle in dieser Gleichung auftretenden Größen kalorimetrisch bestimmt werden; die Integrale können numerisch mittels eines Computers ausgewertet werden.
Eine Schwierigkeit bei der Messung von Entropien ergibt sich daraus,
dass die Bestimmung von Wärmekapazitäten nahe T = 0 sehr
kompliziert ist. Eine theoretisch fundierte Näherung, die oft verwendet
wird, ist die Annahme der Proportionalität zwischen Wärmekapazität
und der dritten Potenz der Temperatur bei tiefen Temperaturen. Diese Beziehung
liegt dem Debyeschen T3-Gesetz zugrunde, welches zur
Extrapolation der Wärmekapazität über den experimentell
nicht erfassbaren Bereich bis zum absoluten Nullpunkt der Temperatur
dient: Cp wird soweit wie möglich gemessen, und eine Kurve
der Form Cp = aT3 wird an die Messwerte angepasst.
Daraus wird der Wert des Parameters a bestimmt und Cp bis auf
T = 0 extrapoliert.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.