In vielen Prozessen spielt die Autokatalyse eine wichtige Rolle, wobei die nachfolgende mathematische Behandlung nícht auf chemische Reaktionen beschränkt ist. Entscheidendes Merkmal einer autokatalystischen Reaktion ist, dass ein Edukt auch als Produkt gebildet wird:
A + B → P + 2B
wobei duch die Reaktion mehr B gebildet als verbraucht wird. Bei einer Atombombenexplosion wird Uran U durch ein Neutron n gespalten, wobei 2 Neutronen frei werden (U+n→2n+Rest), die nun 2 Urankerne spalten können, was zu 4 Neutronen führt, die wiederum....
Die Reaktion kann mit sehr geringen Konzentrationen von B starten, was zunächst eine geringe Geschwindigkeit zur Folge hat. Mit zunehmender Konzentration von B wird die Reaktion jedoch immer schneller. Da aber A verbraucht wird, nimmt die Geschwindigkeit nach Passieren eines Maximums ab.
Die Geschwindigkeitsgesetze lauten:
−d[A]/dt = d[B]/dt = d[P]/dt = k[A][B]
Eine Lösung ist durch Einführen einer Umsatzvaribalen x relativ leicht möglich. Wenn von der Anfangskonzentration a des Edukts A die Menge x verbraucht wird, dann nimmt die Anfangskonzentration b von B um die gleiche Menge zu:
[A](t) = a − x , [B](t) = b + x , [P](t) = x (falls [P]t=0 = 0)
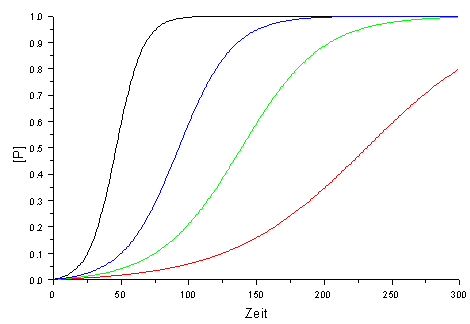 |
| Abb. 1: Konzentrationsanstieg des Produktes P ([P]=[B]-b) als Funktion der Zeit für unterschiedliche Geschwindigkeitskonstenten k. Der Anfangswert von B beträgt 1% der Anfangskonzentration von A (b=0.01a). |
Damit erhalten wir sofort
dx/dt = k (a − x)(b + x)
Diese DGL können wir nach Separation der Variablen integrieren und erhalten schließlich:
[B] = (a + b)/1 + (a/b)·e−(a+b)kt
Für t = 0 ist [B](t=0) = b und führ für t →∞ ist [B] = a + b. Die Abbildung 1 zeigt den typischen Verlauf von [P]=[B]-b für unterschiedliche Geschwindigkeitskonstanten k, wobei die Anfangskonzentration b von B nur 1/100 der von A entspricht: b = a/100.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.