Bei einer bimolekularen Reaktion stossen die beiden Edukte A und B reaktiv
zusammen, was zu den Produkten C und D führt:
| A + B → C + D |
Die Geschwindigkeit berechnet sich nach:
| − d[A]/dt = − d[B]/dt = d[C]/dt = d[D]/dt = k2 [A] [B] |
k2 ist dabei die Geschwindigkeitskonstante der Reaktion mit der Einheit cm3·Molekül−1·s−1 (Molekül−1 kann auch weggelassen werde). Die Einheiten von [A] und [B] sind dann Molekül−1·cm−3.
Ein spezieller Fall der bimolekularen Reaktion ist die "Selbstreaktion"
A + A → C + D
die zu den Geschwindigkeitsgesetzen
− ½ d[A]/dt = d[C]/dt = d[D]/dt = k2[A]²
führt. Die Lösung für [A] ist relativ einfach:
d[A]/[A]² = −2k2 dt
Integration von [A]o bis [A] für die Zeit von t = 0
bis t ergibt:
| 1/[A]o − 1/[A] = −2k2t |
Fragen wir nun nach der Halbwertzeit, d.h. nach der Zeit t½
bei der nur noch die Hälfte der Ausgangssubstanz, [A] = [A]°/2,
vorhanden ist, dann ergibt eine einfache Rechnung:
| t½ = 1/2k2[A]o |
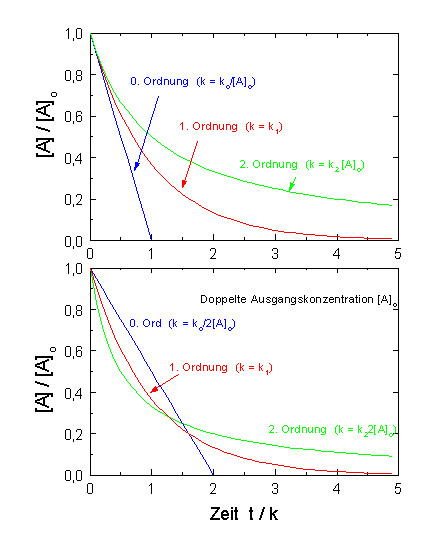 |
| Abb.1: Der zeitliche Verlauf einer Reaktion 0., 1., bzw. 2. Ordnung. Im unteren Bild ist die Anfangskonzentration [A]o verdoppelt worden. Nur die Reaktion 1. Ordnung ist unabhängig von [A]o. |
Die Halbwertszeit ist also umgekehrt proportional zur Ausgangskonzentration
[A]o.
Wir erkennen hier den drastischen Unterschied zu einer Reaktion 1.
Ordnung, bei der die Halbwertszeit unabhängig von der
Ausgangskonzentration war.
In der Abbildung 1 ist der zeitliche Verlauf für eine Reaktion 0., 1. und 2. Ordnung dargestellt. Um einen direkten Vergleich zu ermöglichen, ist im oberen Bild für die Geschwindigkeitskonstante der Reaktion 0. Ordnung k = ko/[A]o, für eine Reaktion 1. Ordnung k = k1 und für eine Reaktion 2. Ordnung k = k2[A]o gesetzt.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.