Manchmal hat die Autokatalyse zur Folge, dass eine Reaktion oszilliert (der Effekt ist der Rückkopplung in elektrischen Schwingungen verwandt); dabei treten räumliche oder zeitliche periodische Änderungen der Konzentrationen der Anfangssubstanzen und der Produkte auf.
Periodische Änderungen der Populationen kennt man in der Biologie aus einfachen Jäger-Beute-Mechanismen, z.B. werden die Kanninchen (Beute) von Füchsen (Jägern) gefressen. Die Population der Füchse nimmt bei diesen reichlichen Nahrungsangebot immer mehr zu. In der Folge nimmt jedoch die Kanninchenzahl ab, da sie von den Füchsen verspeist werden. Bei weniger Kanninchen fehlt dann den Füchsen die Nahrung und deren Zahl nimmt ab, was wiederum den Kanninchen erlaubt ihre Population zu erhöhen. Dann beginnt der Zyklus erneut. Ähnlich erklärt man auch Wirtschaftszyklen (Depression-Wachstum) anhand des "Schweinezyklus":
Ist das Schweineangebot gering, dann ist der Preis für Schweine hoch und die Tierzüchter setzen auf die Schweinezucht, da sie ja ein hoher Verkaufserlös lockt. Da dies viele Züchter tun (schließlich sind alle klug und wollen Geld verdienen), kommt es zu einem Überangebot an Schweinefleisch und der erzeilbare Preis ist gering. Dies hat zur Folge, dass es sich für die Züchter nicht mehr lohnt, Schweinefleisch zu produzieren. Dadurch nimmt jedoch das Angebot wieder ab und der Preis steigt erneut, worauf die Tierzüchter auf die Idee kommen, mit Schweinen viel Geld zu verdienen....
Die Dynamik solcher Prozesse kann mit dem Lotka-Volterra-Mechanismus
beschrieben werden, wobei im Folgenden X für die Beute (Kanninchen)
oder für die Nachfrage (Schweinepreis) steht und Y für die Jäger
(Füchse) oder für das Angebot (Schweinezahl):
| X → 2 X | (1) |
| X + Y → 2 Y | (2) |
| Y → B | (3) |
Der letzte Schritt (3) beshreibt den natürlichen Tod der Füchse, bzw. die Pleite/Geschäftsaufgabe des Züchters. Die ersten beiden Schritte verlaufen autokatalytisch. Für die entsprechende Differentialgleichungen erhalten wir:
d[X]/dt = k1[X] − k2[X][Y]
d[Y]/dt = k2[X][Y] − k3[Y]
Es handelt sich um ein gekoppeltes DGL-System, das nicht mehr geschlossen
gelöst werden kann. Eine numerische Lösung ist in der Abbildung
dargestellt.
 |
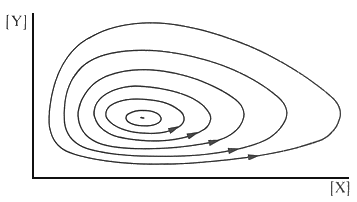 |
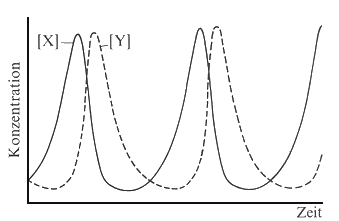
| Abb. 1: Die periodische Änderungen der Konzentration der Zwischenprodukte X und Y in einer Lotka-Volterra- Reaktion. Das System ist nicht im Gleichgewicht, sondern in einem stationären Zustand. | Abb. 2: Die periodischen Änderungen von [X] und [Y] lassen sich auch darstellen, indem man [Y] gegen [X] aufträgt. Das System durchläuft dann geschlossenen Bahnen und kehrt immer wieder zum Ausgangspunkt zurück. Die verschiedenen Bahnen ergeben sich aus verschiedenen Ausgangsbedingungen. |
Sehr instruktiv ist auch eine Darstellung von [Y] gegen [X], denn so wird der periodische Charakter durch geschlossene Bahnen deutlich, wobei unterschiedliche Ausgangsbedingungen zu unterschiedlichen Bahnen führen.
Der Lotka-Volterra-Mechanismus zeichnet sich durch einfache instruktive Prozesse bzw. Gleichungen aus. Die bisher untersuchten chemischen Reaktionen verlaufen allerdings nach etwas komplizierteren Mechanismen.
Eine der ersten oszillierenden Reaktionen, die genauer untersucht wurden, war die schon erwähnte Bjelousow-Shabotinski-Reaktion. Die Reaktionsmischung besteht aus einer suaren Lösung von Kaliumbromat, Malonsäure und einem Ce(IV)-Salz. Richard Noyes hat ihren Mechanismus aufgeklärt, an dem in 18 Einzelschritte insegesamt 21 verschiedene chemische Teilchenarten beteiligt sind. Die wichtigsten Aspekte dieses kompliezierten Mechanismus lassen sich durch ein Gleichungssystem beshreiben, das den Namen Oregonator trägt (Noyes lebt in US-Staat Oregon). Wir verwenden die Abkürzungen X für HBrO2, Y für Br− und Z für 2Ce4+:
A + Y → X, X + Y → C, B + X → 2X + Z, 2X → D, Z → Y.
Die Konzentrationen von A, B, C und D werden in diesem Modell als konstant
angesehen. Entscheiden ist die Autokatalyse im dritten Schritt und die
Rückkopplung mit den anderen Schritten.
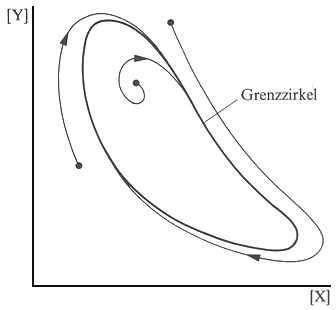 |
| Abb. 3: Bei manchen Reaktionen wird, unabhängig von den Startbedingungen, nach einiger Zeit immer die gleiche geschlossene Bahn erreicht. Diese Bahn heisst Grenzzirkel. |
Oszillierende Reaktione sind keineswegs nur eine Kuriosität zu Demonstrationszwecken. Bei industriellen Prozessen treten sie bisweilen auf, aber es gibt viele Beispiele für solche Reaktionen in biochemischen Systemen, bei denen die lebende Zelle die Rolle des chemischen Reaktorsd übernimmt. Die Erregung der Herztätigkeit z.B. kommt durch oszillierende Reaktionen zustande. Man beobachtet sie aber auch bei der Glykolyse, bei der aus einem Molekül Glukose (über enzymkatalysierte Reaktionen, an denen ATP beteilgt ist) zwei Moleküle ATP synthetisiert werden. Alle Stoffwechselprodukte der Reaktionskette oszillieren unter gewissen Bedingungen mit derselben Frequenz, aber mit unterschiedlicher Phase.
Oszillierende Reaktionen erfreuen sich gegenwärtig einer großen
Aufmerksamkeit; man versucht, über die Autokatalyse hinaus ihre tieferen
Ursachen zu ergründen. Es scheint, dass für ihr Auftreten
drei Bedingungen erfüllt sein müssen:
| (1) | Die Reaktionen müssen weit entfernt vom Gleichgewichtszustand ablaufen |
| (2) | Die Reaktionen müssen autokatalystische Schritte enthalten |
| (3) | In dem System müssen zwei stationäre Zustände auftreten |
Das letzte Kriterium nennt man Bistabilität; damit sind Eigenschaften verbunden, die sich erheblich von denen unterscheiden, die wir an Systemen im oder nahe am Gleichgewicht beobachten.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.