Durch Beobachtung des solaren UV-Spektrums stellte man bereits um 1920 fest, dass sich Ozon in der Stratosphäre befinden muss. Eine erste theoretische Begründung geht auf Sydney Chapmann zurück, der damit den Grundstock für unser heutiges Verständnis des stratosphärischen Ozons legte.
Wir haben bereits den Abbau des Ozons durch die UV-Strahlung der Sonne kennengelernt:
O3 + hν (l< 310 nm) → O + O2 J1
Danach ist nach wenigen Minuten das Ozon abgebaut. Doch es gibt nicht nur diesen Abbaumechanismus, sondern auch einen Aufbaumechanismus für Ozon - schließlich muss es irgendwo herkommen. Es ist die Reaktion eines Sauerstoffatoms mit einem Sauerstoffmolekül:
O + O2 + M → O3 + M k3
wobei noch ein dritter Stosspartner M (in der Atmosphäre N2 oder O2) erforderlich ist, um den Stosskomplex O − O2 zu stabilisieren. Näheres zu solchen Dreikörperreaktionen gibt es hier. Unter atmosphärischen Bedingungen kann man die Ozonaufbaurate danach durch
d [O3]/dt = k3 [O][O2][M]
beschreiben.
Diese beiden Prozesse laufen relativ schnell ab und bestimmen das Gleichgewicht für das gelten muss:
Ozonabbau = Ozonaufbau
J1 [O3] = k3 [O][O2][M]
| [O]/[O3] = J1/k3[O2][M] | (1) |
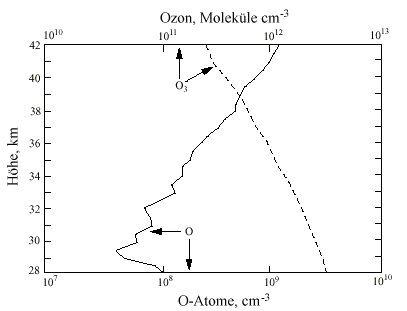 |
| Abb. 1: Gleichzeitige Messung der Ozon-Konzentration über Texas |
Da [O2] und [M] mit der Höhe abnehmen, muss das Verhältnis
[O]/[O3]
entsprechend zunehmen, was Messungen von [O] und [O3] auch bestätigen
(Abb. 1). Das Sauerstoffatom entsteht aber nicht nur über die Photolyse
von Ozon, sondern zusätzlich - wenn auch zu einem geringen Ausmaß
- durch die Photodissoziation von O2:
| O2 + hν (l< 230 nm) → O + O | J2 |
d[O]/dt = J2[O2]
Die Photolyserate ist durch den kleineren Absorptionsquerschnitt und
den geringeren Photonenfluss bei diesen Wellenlängen um viele Grössenordnungen
kleiner als im Falle des Ozons (J1), was Abb. 2 zu entnehmen
ist.
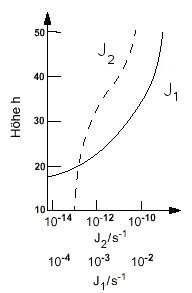 |
| Abb. 2: Photolyseraten von O2 (J2) und O3 (J1) bei unterschiedlichen Höhen h. |
| O + O3 → 2O2 | k2 |
d[O]/dt = −k2[O][O3]
Nach diesen beiden Gleichungen gilt für das Gleichgewicht:
J2 [O2] = k2[O][O3]
Setzen wir in diese Gleichung die O-Konzentration aus der obigen Gleichung
(1) ein, dann erhalten wir:
| [O3] = (J2 k3[M]/J1 k2)½ [O2] | (2) |
Die Gleichung ist verblüffend einfach, dennoch ist es nicht ganz
einfach, hieraus die Ozon-Konzentration zu berechnen, da die Photolyseraten
J1 und J2 bei der Höhe h vom aktinischen Fluss
Iλ (h) abhängen, der wiederum
durch Absorption der Strahlung durch darüberliegende O2
und O3 Schichten beeinflusst wird.
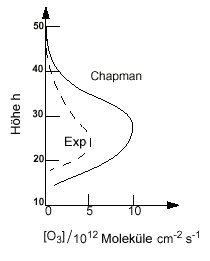 |
| Abb. 3: Berechnete (durchgezogene Linie) und experimentell beobachtete (gestrichelte Linie) vertikale Profile der Ozonkonzentration. |
Daher kann man die Gleichung (2) nur numerisch lösen, indem man beim oberen Ende der Atmosphäre mit [O3] = 0, einer niedrigen O2-Konzentration, und dem aktinischen Fluss, der durch die Sonne und den Einfallswinkel auf die Erde bestimmt ist, beginnt, und dann in kleinen Intervallen zu tieferen Schichten der Atmosphäre geht und dabei Iλ (h) und die Werte für J1 (h), J2 (h) und [O3] (h) berechnet. Das Ergebnis ist in Abb. 3 dargestellt und beschreibt den Verlauf der O3-Konzentration bei unterschiedlichen Höhen qualitativ sehr gut, wie aus dem Vergleich mit den beobachteten Werten (gestrichelte Kurve in Abb. 3) hervorgeht. Allerdings ist die tatsächliche Ozonkonzentration um mehr als den Faktor 2 geringer als der Chapman-Mechanismus erklärt. Dies deutet auf weitere O3-Senken hin.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.