Die Formel für die Freie Enthalpie eines Systems aus unabhängigen Teilchen lautet:
G − G(0) = − nRT ln(qm/NA)
wobei qm die molare Zustandssumme q/n ist. Der Zusammenhang zwischen der Gleichgewichtskonstanten Kp und der Freien Standardenthalpie ist:
Δr Go
= − RT ln Kp
Wenn es gelingt, diese beiden Gleichungen zu verknüpfen, können wir die Gleichgewichtskonstante berechnen.
Zuerst brauchen wir die molare Freie Enthalpie für die einzelnen
Komponenten, nämlich G/n, dann deren Standardwert.
Das heißt, wir suchen den Wert der molaren Zustandssumme für
p = po = 1 bar; diesen Wert bezeichnen wir
mit qmo. Weil nur der Translationsanteil
vom Druck abhängt (über Vm = V/n),
können wir qm mit Vm = RT/po
berechnen. Dann erhalten wir für die Komponente J
GJ,mo −
GJ,mo(0) = −
RT ln (qJ,mo/NA)
ist die Freie Standardenthalpie gegeben durch
Δr Go
= ΣJ νJ
GJ,mo = ΣJνJ
GJ,mo(0)
−
RT ΣJνJ
ln (qJ,mo/NA)
Mit G(0) = U(0) können wir für den ersten Summanden auf der rechten Seite auch schreiben
ΣJ νJ
GJ,mo(0) = Δr
Go(0) = Δr
Uo(0)
Die Reaktionsenergie bei T = 0 ist die Differenz zwischen den (molaren) Nullpunktsenergieniveaus der an der Reaktion beteiligten Komponenten (natürlich mit den stöchimetrischen Koeffizienten gewichtet), wofür wir immer ΔE0 geschrieben haben:
ΔE0 = Δr
Uo(0)
Jetzt können wir die Gleichung für Δr
Go vereinfachen:
Δr Go
= ΔE0 −
RT ΣJ ln (qJ,mo/NA)νJ
Δr Go
= − RT {−ΔE0/RT
−
ln ΠJ(qJ,mo/NA)νJ}
Vergleichen wir diesen Ausdruck mit der Gleichung Δr
Go = − RT ln Kp,
dann erhalten wir eine Beziehung für Kp:
Kp = − ΔE0/RT
+ ln ΠJ (qJ,mo/NA)νJ
Daraus folgt
Kp = {ΠJ(qJ,mo/NA)νJ}
e−ΔEo/RT
Die Anwendung dieser Formel wollen wir an einem Beispiel demonstrieren. Ein zweiatomiges Molekül soll in seine Atome dissoziieren: X2(g) ↔ 2X(g). Wir schreiben diese Reaktion in der Form
0 = 2X(g) − X2(g), νX = 2, νX2 = −1
Dann lautet die Gleichgewichtskonstante bezogen auf die Zustandssummen
Kp = (qX,mo/NA)2(qX2,mo/NA)−1
e−ΔE0/RT
Kp = {(qX,mo)2/qX2,moNA}
e−ΔE0/RT
ΔE0 isz die molare Dissoziationsenergie D0 des Moleküls (bezogen auf die Energie der Nullpunktsschwingung von X2). In der Zustandssumme der Atome kommt nur die Translationsbewegung und eventuell eien elektronische Entartung vor:
qX,mo = gX(Vmo/ΛX3),
Vmo = RT/po
Für das zweiatomige Molekül aber müssen wir auch die Rotations- und Schwingungsfreiheitsgrade berücksichtigen:
qX2,mo
= gX2 (Vmo/ΛX23)
qr,X2 qv,X2
Damit erhalten wir für die Gleichgewichtskonstante
Kp = (gX2/gX)(ΛX23 Vm0/ΛX6NA)(1/qr,X2 qv,X2) e−D0/RT
für das Beispiel Na2(g) ↔ 2Na(g) kennen wir alle Parameter und im folgenden Beispiel werden wir die Gleichgewichtskonstante für Na2(g) ↔ 2Na(g) bei 1000 K berechnen. Die folgenden spektroskopischen Daten werden benötigt: B = 0,1547 cm−1, v~ = 159,2 cm−1, D0 = 70,4 kJ mol−1 (0,73 eV). Für Na ist Mr = 22,99. Der Grundterm der Atome ist zweifach entartet.
Zunächst berechnen wir die Zustandssummen und dann Kp.
Wenn wir die angegebenen Zahlenwerte in die Formel einsetzen, dann erhalten
wir
| ΛNa23 = 5,40 · 10−34 m3 | ΛNa3 = 1,53 · 10−33 m3 | ||
| qr,Na2 = 2246 | qv,Na2 = 4,885 | gNa = 2 | gNa2 = 1 |
Mit Vmo = 8,314 · 10−2
mol−1 schließlich Kp
= 2,45.
Nach diesem Verfahren erhält man Kp. Man kann das Ergebnis
aber mit [J] = pJ/RT leicht in die Konzentration
umrechnen.
 |
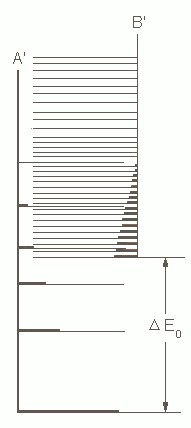 |
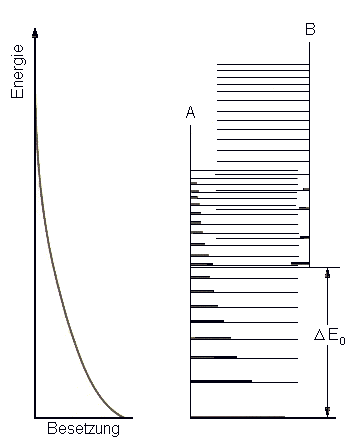
| Abb. 1: Die Energieniveaus der Komponenten A und B. Im Gleichgewicht sind alles Niveaus zugänglich, deshalb ergibt sich die Gleichgewichtszusammensetzung aus der Boltzmann-Verteilung über alles Zustände. Bei steigendem ΔE0 wird A vorherrschend. | Abb. 2: Hier kommt es auf die Zustandsdichte an. Zwar liegt B weit oberhalb von A (DE0 ist groß und positiv), die Anzahl seiner Zustände ist aber so groß, dass B in der Mischung dominiert. Dem entspricht in der klassischen Thermodynamik, dass wir zur Berechnung von Gleichgewichten nicht nur die Enthalpien, sondern auch die Entropien berücksichtigen müssen. |
Wir sind jetzt in der Lage, Gleichgewichtskonstanten physikalisch zu interpretieren. Betrachten wir das einfache Gleichgewicht A ↔ B. In Abbildung 1 sind zwei Gruppen von Niveaus eingezeichnet; die einen gehört zu A, die andere zu B. Die Besetzungszahlen ergeben sich aus der Boltzmannschen Verteilungsformel; sie hängen nicht davon ab, ob ein bestimmtes Niveau zu A oder B gehört. Wir können uns deshalb vorstellen, dass die Niveaus beider Gruppen ohne Unterscheidung nach A oder B gemäß einer einzigen Boltzmann-Verteilung besetzt werden. Sind, wie in Abbildung 1, die Abstände zwischen den A- und B-Niveaus ähnlich und liegt B oberhalb von A, dann wird in der Gleichgewichtsmischung A überwiegen. Wenn jedoch die Zustandsdichte von B, wie in Abbildung 2 , wesentlich höher ist, dann überwiegt im Gleichgewicht B, obwohl es die höhere Nullpunktsenergie hat.
Mann kann aus Diagrammen wie denen in Abbildung 1 und 2 Formeln für die Gleichgewichtskonstanten in Abhängigkeit von den Zustandssummen herleiten. Der Zustand i in dem System mit dem Komponenten A und B hat die Besetzungszahl
ni = N (e-bei) 1/q
wobei N die Anzahl der insgesamt vorhandenen Moleküle angibt (β = 1/kT). Zur Komponente A sollen NA Moleküle, zu B NB Moleküle gehören. Zur Berechnung von NA hat man die Besetzungszahlen der Zustände Ea, die jeweils zu A gehören, aufzusummieren; NB ist die Summe über E'b:
NA = Σi(A) ni = (N/q)aΣ e-bEa, NB = Σi(B) ni = (N/q)bΣ e-bE'b
Die Summe über alles Zustände von A ist aber nichts anderes als die Zustandssumme von A, es gilt also NA = NqA/q. Die Summe über die Zustände von B ist ebenfalls eine Zustandssumme, die Energiewerte sind aber auf den Grundzustand des Gesamsystems, der mit dem Grundzustand von A identisch ist, bezogen. Wenn wir mit De0 = ΔE0/NA die Differenz der Nullpunktsenergien der beiden Komponenten bezeichnen, (Abb. 1), können wir E'b = Eb + De0 schreiben und erhalten
NB = (N/q)bΣ e−(Eb + De0)β = (NqB/q) e−ΔE0/RT
Die Gleichgewichtskonstante der Reaktion A ↔ B ist dem Verhältnis der beiden Komponenten proportional; es folgt also
Kp = NB/NA = {qB/qA} e−ΔE0/RT
und das ist identisch mit unserer allgemeinen Gleichung für die
Gleichgewichtskonstante (für das Gleichgewicht A ↔
B heben sich die Faktoren mit V in den Zustandssummen heraus; es wird also
nichts geändert, wenn man q anstelle von qo
schreibt. Allgemein kann man von q auf qo übergehen,
wenn man Kp wie dimensionslose Zahlen behandelt.)
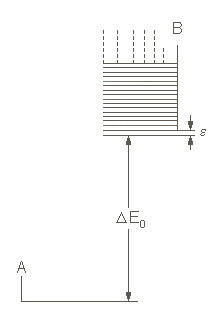 |
| Abb. 3: Das im Text verwendete Modell zur Berechnung der Einflüsse der Energieabstände und der Zustandsdichten auf die Gleichgewichte. B kann dominieren, solange ΔE0 nicht zu groß wird. |
Die Aussage der letzten Gleichung läßt sich verdeutlichen, wenn man einmal ein System betrachtet, bei dem für A nur ein einziger Zustand zugänglich ist, so dass qA = 1 wird, und bei dem B sehr viele sehr dicht beieinander liegende Niveaus hat (Abbildung 3). Die Zustandssumme von B lautet dann
qB = 1/{1 − e-be} = 1/{1 − (1 -be + ....)}≈ 1/be = kT/ε
Daraus folgt für die Gleichgewichtskonstante des Gleichgewichts A B
Kp = (kT/ε) e−ΔE0/RT
Wenn ΔE0 sehr groß ist, dominiert der Exponentialterm, und es wird Kp ≈ 0; im Gleichgewicht ist also nur sehr wenig B vorhanden. Wenn ΔE0 klein, aber noch positiv ist, kann Kp größer als Eins werden, weil B wegen der höheren Zustandsdichte im Gleichgewicht überwiegen kann. Bei tiefen Temperaturen wird Kp ≈ 0, denn dann besteht das System vollständig aus A. Bei hohen Temperaturen gehen die Exponentialausdrücke gegen Eins, und der Faktor davor wird groß. Auch in diesem Fall nimmt B zu. Die Reaktion ist endotherm (weil B energetisch über A liegt), deshalb begünstigt eine Temperaturerhöhung die Bildung von B, denn es werden mehr Zustände zugänglich.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.