Wir haben am Beispiel des Chloratoms gesehen, wie bei einem Zweiniveau-System die thermodynamischen Funktionen mit Hilfe der Zustandssumme q ausgerechnet werden können. Dies war relativ einfach (aber kompliziert genug), da die Energien und Entartungen der beiden Niveaus bekannt waren. Doch wieviele Energiezustände gibt es bei der Translation und wieso sollte die Energie entartet sein? Ist die Translation nicht kontinuierlich und sollte es daher nicht unendlich viele Zustände geben? Die exakte Antwort auf all diese Fragen gibt die Quantenmechanik in der Behandlung eines Teilchens in einem Würfel mit dem Volumen V. Im Folgenden soll das wesentliche Ergebnis über einen etwas "schlampigen" Weg abgeleitet werden:
Zunächst müssen wir uns vor Augen führen, dass die Bewegungen in x-, y- und z-Richtung äquivalent und unabhängig von einander sind, d.h. die Zustandssumme der Translation ist qt = qx · qy · qz = qx³ = qy³ = qz³. Wir betrachten daher nur eine Richtung (Dimension). Die Quantenmechanik lehrt uns, dass es den Welle-Teilchen-Dualismus gibt, d.h. wir müssen alles nicht nur als Teilchen sondern auch als Welle verstehen. Die Wellenlänge hat deBroglie sehr einfach berechnet, indem er (zurecht) annahm, dass die Beziehung für Photonen mit der Lichtgeschwindigkeit c, E = hν = mc² Þh/λ = mc = p, für jede beliebige Materie mit der Masse m und Impuls p gilt:
 |
p = h/λ
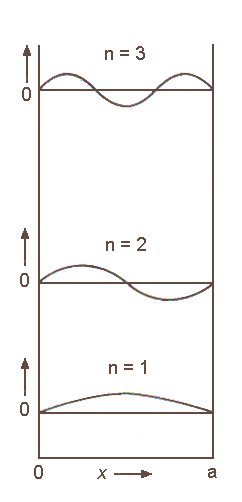
Wenn wir eine Welle auf eine Länge x einsperren (siehe Abbildung) dann passen nur bestimmte stehende Wellen hinein für die gilt
nxλ/2 = x,
wobei nx eine ganze Zahl ist. Damit erhalten wir für den Impuls p = nx · h/2x und für die Energie E = ½mv² = p²/2m = n² h²/8mx² = En.
Das niedrigste Energieniveau liegt bei n = 1 : E1 = h²/8mx². Die Zustandssumme bezogen auf den Energieabstand zum niedrigsten Niveau ist
qt,x = Σnx=1 e−[(n²−1)h²/8mx²]/kT = Σnx=1 e−(n²−1)C
wobei die Konstante C = h²/8mx²kT ist.
Die Summation können wir durch eine Integration ersetzen, da die Niveaus sehr eng beieinander liegen:
qt,x = 1ò¥ e−C(n²−1)dn ≈0ò¥ e−Cn²dn = (π/C)½/2
Einsetzen von C ergibt sofort
qt,x = (π8mx²kT/h²)½/2
= x(2πmkT/h²)½
oder
qt,x = x/Λ mit Λ = (h²/2πmkT)½
Damit erhalten wir für die Zustandssumme der Translation:
qt = qt,x · qt,y · qt,z = x · y · z (2πmkT)3/2/h³
| qt = V · (2πmkT/h²)3/2 |
Λ wird thermische Wellenlänge genannt. Wenn Λ klein gegenüber der mittleren Entfernung zwischen den Molekülen ist, dann kann die Boltzmann-Statistik, so wie wir sie bisher behandelt haben, verwendet werden. Bei sehr niedrigen Temperaturen kann Λ jedoch immer größer werden und wir müssen dann, je nach Teilchentyp, entweder die Bose-Einstein-Statistik (Bosonen: Teilchen mit ganzzahligen Spin) oder die Fermi-Dirac-Statistik (Fermionen: Teilchen mit halbzahligen Spin) verwenden. Durch Laserkühlung erreicht man heute Temperaturen von 10−6 K, was eine grosse thermische Wellenlänge zur Folge hat und damit zu einem neuartigen (kollektiven) Verhalten der Teilchen führt. Momentan sind Untersuchungen hierzu ein höchst aktuelles Forschungsgebiet (Bose-Einstein-Kondensation).
Der Beitrag der Translation zur inneren Energie U eines idealen Gases können wir nun sofort ausrechnen, indem wir die Zustandssumme qt in die Bestimmungsgleichung für U einsetzen:
Ut = NkT² ∂lnq/∂T = NkT² ∂/∂T(3/2 lnT + ln[(2πmk/h²)3/2V])
| Ut = 3/2 NkT |
Da Nk = nNAk = nR ist, wobei n die Molzahl angibt, ist Ut,m = 3/2 RT für 1 Mol und die spezifische Wärme CV,m = ∂Ut/∂T = 3/2 R. Den Druck können wir über die Beziehung p = NkT ∂lnqt/∂V = NkT/V berechnen, woraus pV = nRT folgt. Den Beitrag der Translation zur Entropie berechnen wir (für ununterscheidbare Teilchen) gemäss:
St = Nk [T ∂lnqt/∂T + ln qt/N + 1]
St = Nk [ln{(2πmkT/h²)3/2 · V/N} + 5/2]
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.