Um den Umgang mit Zustandssummen etwas besser kennenzulernen, wollen wir uns ein (etwas exotisches) Beispiel ansehen, bei dem nur zwei Zustände beteiligt sind. Bei Halogenatomen setzt sich der elektronische Grundzustand, ²P, aus zwei getrennten Niveaus (Zuständen) zusammen. Der energetisch niedrigste Zustand (E1 = 0) ist der ²P3/2-Zustand der 4-fach entartet ist (g1 = 4). Das zweite Energieniveau ²P1/2 liegt um den Betrag ΔE oberhalb des energetisch niedrigsten Zustandes und ist 2-fach entartet (g2 = 2). Die elektronische Zustandssumme qe ist also
qe = Σi gi e−Ei/kT = g1e−E1/kT + g2e−E2/kT
| qe = 4 + 2e−ΔE/kT |
Die letzte Gleichung ergibt sich einfach durch Ensetzen des Werte g1 = 4, E1 = 0, g2 = 2, E2 = ΔE. Die Grösse ΔE hängt vom Halogenatom ab und beträgt z.B. für F-Atome: ΔE(F) = 404 cm−1, für Cl-Atome: ΔE(Cl) = 882 cm−1 und für Iod-Atome: ΔE(I) = 8000 cm−1. Der Verlauf von qe als Funktion der Temperatur T ist für Chlor-Atome in der Abbildung 1 dargestellt. Für T → 0 wird die e-Funktion unendlich gross, d.h. qe(T→ 0) → 4. Für sehr hohe Temperaturen (T >> DE/k) gilt ΔE/kT→ 0 und damit für die Zustandssumme qe(T→∞) ® 6. (Bei extrem hohen Temperaturen können auch höhere elektronische Zustände angeregt werden. Diese liegen jedoch bei einigen 10000 cm−1, so dass erst bei Temperaturen von mehreren 10000 K diese Zustände berücksichtigt werden müssen).
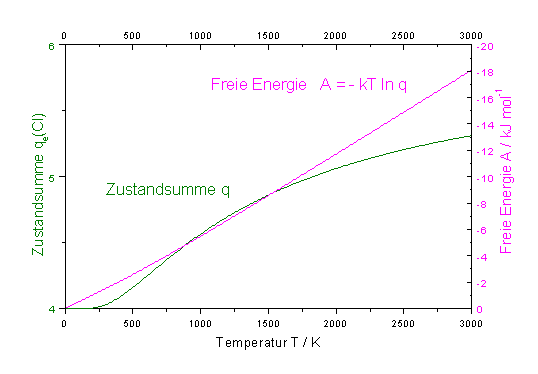 |
| Abb. 1: Verlauf der
Zustandssumme qe und der freien Energie Ae
für den elektronischen
Anteil von 1 mol Cl-Atome. |
Der Beitrag der elektronischen Energie zur freien Energie Ae ist dann:
| Ae = - NkT ln qe = - NkT ln[4+2e−ΔE/kT] |
Der Verlauf von Ae als Funktion der temperatur ist ebenfalls in Abbildung 1 dargestellt.
Der Beitrag der elektronischen Energie zur inneren Energie Ue berechnet sich zu:
Ue = NkT² ∂(lnqe)/∂T = NkT² ∂(ln[4 + 2e−ΔE/kT])/∂T
Ue = NΔE/(1 + 2eΔE/kT)
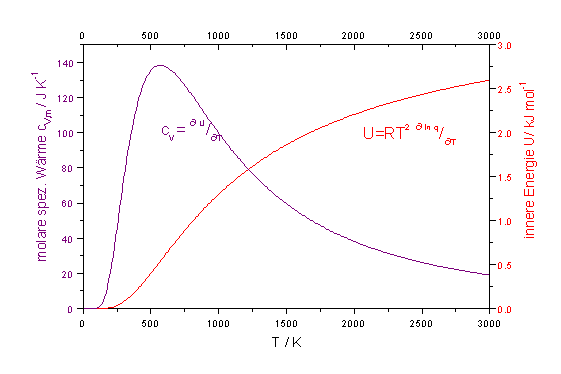 |
| Abb. 2: Verlauf der inneren Energie Ue und der spezifischen Wärme cV für 1 mol Cl-Atome. |
Der Verlauf von Ue als Funktion der Temperatur T ist für Chlor-Atome in der Abbildung 2 dargestellt. Für T → 0 wird die e-Funktion unendlich gross, d.h. Ue(T→ 0) → 0. Für sehr hohe Temperaturen (T >> DE/k) gilt ΔE/kT→ 0 und damit für die innere Energie Ue(T→∞) ® NΔE/3. Den Beitrag der beiden energetischen Zustände zur spezifischen Wärme cV,e erhalten wir gemäss
cV,e = ∂Ue/∂T = (2NΔE²/kT²) eΔE/kT/(1 + 2eΔE/kT)2
Der Verlauf von cV,e ist ebenfalls in Abbildung 2 dargestellt. Abbildung 3 zeigt den Verlauf des elektronischen Anteils zur Enthalpie H = U+pV und zur Entropieals Funktion der Temperatur für 1 mol Cl-Atome.
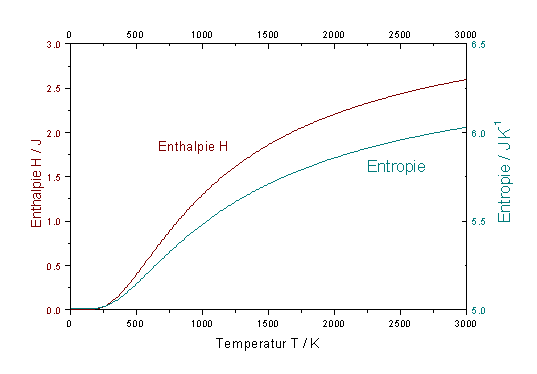 |
| Abb. 3: Verlauf des elektronischen Anteils zur Enthalpie und zur Entropie als Funktion der Temperatur für 1 mol Cl-Atome. |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.