Energieverteilung nach Boltzmann

Wir können natürlich auch die Geschwindigkeitsverteilung F(v) in eine kinetische Energieverteilung G(E) umrechnen (Das Symbol G( ) wurde nur gewählt, um die andere mathematische Form dieser Verteilung hervorzuheben) :

E = ½ mv2 → v  =  (2E/m)½             dE/dv = mv → dv  =  dE/(mv)  =  dE/(2mE)½

Einsetzen in die Maxwell-Verteilung ergibt:
 

 G(E)dE  =  2π(πkT)-3/2 E½e-E/kTdE

Wir wollen nun die mathematische Form der molekularen Verteilungsfunktion für die Energie ableiten, wobei wir von den folgenden Voraussetzungen ausgehen:

Pg(E) = Pg(E1 + E2)  =  P(E1) · P(E2),

wobei das (letzte) Gleichheitszeichen gilt, da wir annehmen, dass die Teilchen unabhängig voneinander sind. Nur die Exponentialfunktion erfüllt diese Gleichung, was nun gezeigt werden soll:

∂Pg/∂E1 = (dP/dE1) · P(E2)  =  (dPg/dE) · (dE/dE1) = dPg/dE

(da dE/dE1  =  d(E1 + E2)/dE1 = 1)

Division durch Pg(E) ergibt:

(1/Pg(E))·(dPg/dE)  =  [1/P(E1)·P(E2)]·[dP/dE1 · P(E2)]  =  (1/P(E1))·(dP/dE1)

 Entsprechend erhält man durch Differenzieren nach E2

(1/Pg(E))·(dPg/dE)  =  (1/P(E2))·(dP/dE2)

Da die jeweils rechte Seite der beiden obigen Gleichungen nur von E1 bzw. E2 abhängt, aber für beliebige E1, E2 gelten muss, führt dieses zu

1/P(E1)· (dP/dE1)  =  β  =  1/P(E2)· (dP/dE2),

wobei β eine Konstante ist. Dies führt auf die Gleichung

dP/P  =  β· dE

Integration ergibt (c ist eine Integrationskonstante):

ln P  =  βE + c     oder     P  ~  eβE

Die Konstante β = -1/kT kennen wir bereits aus der kinetischen Gastheorie.

Die Wahrscheinlichkeit P(E) ein Teilchen mit der Energie E vorzufinden nimmt also exponentiell mit E ab.
 
 

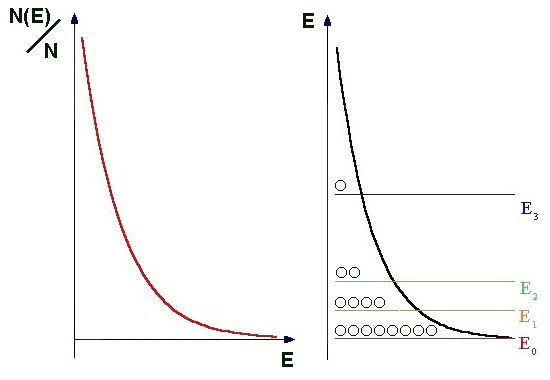Abb.1: Die Wahrscheinlichkeit N(E)/N ein Teilchen bei der Energie E zu finden nimmt exponentiell mit E ab:  N(E) ~ e-E/kT (links). Die rechte Abb. zeigt, wie die Besetzungszahl N(E) - dargestellt durch die Kreise - bei der niedrigst möglichen Energie Eo am größten ist und mit zunehmender Energie exponentiell abnimmt.
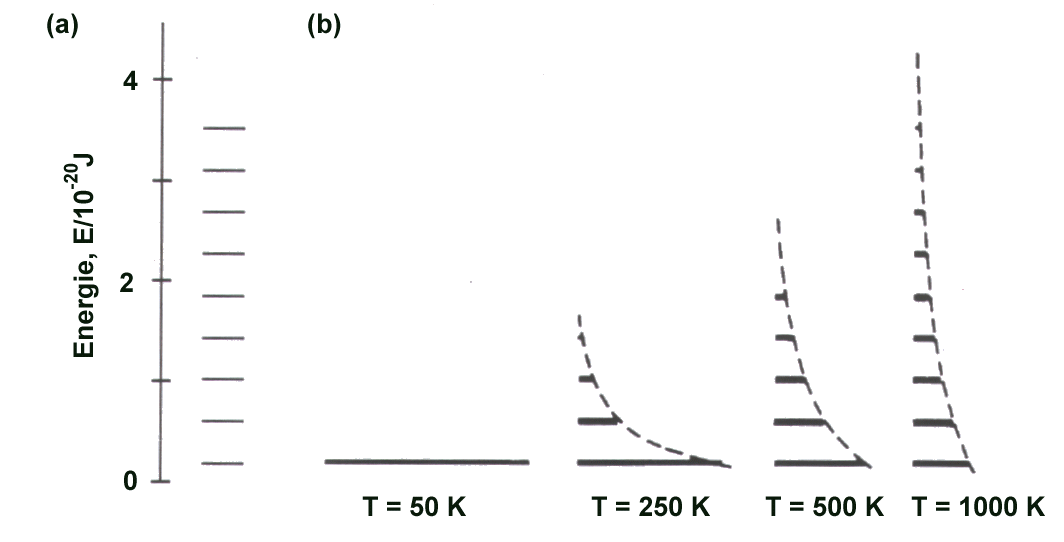Abb. 2: Besetzung der Vibrationsniveaus beim I2-Molekül. a) Energieskala und Vibrationszustände; b) Die Länge der Striche gibt die Zahl der Iod-Moleküle in den einzelnen Vibrationsniveaus wieder.

Wenn wir die Energiewerte kennen, die unsere Teilchen annehmen, dann ist der Bruchteil N(E)/N der Teilchen, die diesen Energiewert besitzen, gegeben durch:
 

N(E)/N  =  e-E/kT /ΣE e-E/kT

Falls die Teilchen unterschiedliche Zustände einnehmen können, die aber die gleiche Energie haben, dann spricht man von der Entartung eines Zustandes. Der Grad der Entartung, d.h. wie viele unterschiedliche Zustände die gleiche Energie E haben, wird mit g(E) bezeichnet. Wir müssen diese Zustände natürlich in unserer Boltzmannverteilung mit berücksichtigen und es gilt ganz allgemein:
 

N(E)  ~  g(E) e-E/kT

Dies ist das Boltzmannsche Energieverteilungsgesetz. Ein einfaches Beispiel zur Entartung ist die Knickschwingung des linearen CO2-Moleküls:   O - C - O
Die Schwingung kann in der Zeichenebene (nach "oben" und "unten") erfolgen oder senkrecht dazu (nach "vorn" oder "hinten"). Die Energie der Schwingung muss gleich sein, also ist die Schwingung zweifach entartet, d.h. g = 2.
Wenn wir uns nun die eingangs abgeleitete Verteilung der kinetischen Energie G(E) ansehen, dann erkennen wir nicht nur die Exponentialfunktion wieder, sondern es taucht auch ein Vorfaktor E½ auf, woraus wir schließen können, dass die Translation mit g(E) ~ E½ entartet ist . Doch diese Beobachtung führt uns direkt in die Statistische Thermodynamik, der es gelungen ist, alle thermodynamischen Erkenntnisse auf eine mikroskopische Sichtweise zurückzuführen.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.