Flüssigkeiten

Bei der Beschreibung von Festkörpern gehen wir stets von der wohlgeordneten Struktur eines idealen Kristalls aus. Die potentiellen Energien sind weit höher als die kinetischen Energien. Bei Gasen ist unser Startpunkt die völlig ungeordnete Bewegung der Moleküle. Hier überwiegen die kinetischen Energien die potentiellen. Flüssigkeiten liegen zwischen diesen beiden Extremen: Es gibt noch eine gewisse Nahordnung, aber kaum eine Fernordnung.

Die Teilchen in einer Flüssigkeit werden durch zwischenmolekulare Kräfte zusammengehalten, ihre kinetischen Energien sind jedoch vergleichbar mit ihren potentiellen Energien. Die ganze Struktur ist daher sehr beweglich. Für eine mathematische Beschreibung müssen wir uns mit den mittleren Positionen der Teilchen begnügen. Die radiale Verteilungsfunktion g ist so definiert, dass g(r)r2dr die Wahrscheinlichkeit angibt, in einem Intervall dr im Abstand r von einem Teilchen ein zweites Teilchens anzutreffen.
Für einen idealen Kristall besteht g(r) aus einer Abfolge von scharfen Peaks, die die festen Positionen der Atome im Kristall angeben. Diese Regelmäßigkeit setzt sich bis an die Grenzen des Kristalls fort, wir sprechen daher von einer Fernordnung der Atome im Kristall. Beim Schmelzen des Kristalls geht diese Fernordnung verloren, und wenn wir in großer Entfernung von einem Teilchen nach der Wahrscheinlichkeit schauen, ein zweites Teilchen anzutreffen, so erhalten wir einen konstanten Wert. In direkter Umgebung eines Teilchens können die nächsten Nachbarn jedoch immer noch ungefähr an ihren alten Positionen sitzen, und selbst wenn sie durch neue Atome ersetzt werden, werden diese mit einiger Wahrscheinlichkeit die Positionen der alten besetzen. Wir können daher auch in der Flüssigkeit noch eine Schale von nächsten Nachbarn eines Atoms bei einem Abstand r1 finden, und in etwas größerer Entfernung vielleicht auch noch eine Schale mit übernächsten Nachbarn bei einem Abstand r2. Diese Erscheinung bezeichnen wir als Nahordnung. Für die radiale Verteilungsfunktion bedeutet das, dass sie bei kurzen Abständen oszilliert, bei r1 ein Maximum besitzt, bei r2 ein zweites, aber weniger ausgeprägtes Maximum, vielleicht noch weitere bei größeren Abständen, und dann für sehr große Abstände gegen einen konstanten Wert geht.
 
 
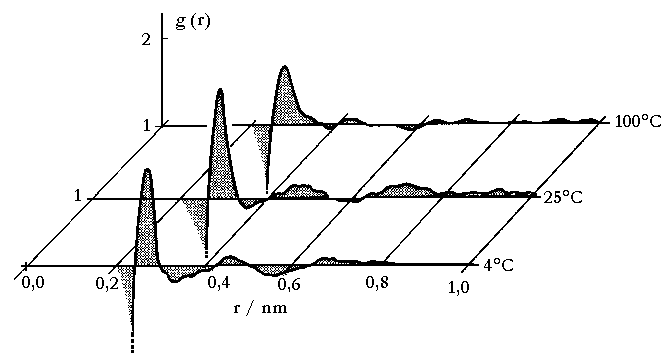Abb. 1: Die radiale Verteilungsfunktion der Sauerstoffatome in flüssigem Wasser bei drei Temperaturen. Mit steigender Temperatur verschieben sich die Maxima nach außen.
Wir können die Form der radialen Vereilungsfunktion durch Röntgenbeugung bestimmen. Sie kann aus dem für flüssige Proben typischen unscharfen Beugungsmuster in ganz ähnlicher Weise abgeleitet werden wie eine Kristallstruktur aus den scharfen Röntgenreflexen der Kristalle. Die lokale Schalenstruktur ist ohne weiteres zu erkennen, wie es die in der Abbildung dargestellte Verteilungsfunktion für Wasser zeigt. Eine genauere Analyse ergibt, dass in der Flüssigkeit jedes Wassermolekül tetraedrisch von vier anderen Wassermolekülen umgeben ist. Die gezeigte Verteilungsfunktion für 100°C beweist auch, dass die zwischenmolekularen Kräfte (in diesem Fall hauptsächlich Wasserstoffbrücken) stark genug sind, diese lokale Struktur bis zum Siedepunkt aufrechtzuerhalten.
Die radiale Verteilungsfunktion können wir berechnen, wenn wir die Form des zwischenmolekularen Potentials kennen. Der Vergleich zwischen berechneter und gemessener Verteilungsfunktion ist daher ein wichtiger Test für Theorien der Struktur der Flüssigkeiten. Man findet allerdings, dass eine aus harten Kugeln bestehende Flüssigkeit ausgeprägtere Oszillationen der radialen Verteilungsfunktion zeigt als jede andere Art von Flüssigkeit bei gleicher Temperatur. Die Tatsache, dass sowohl attraktive als auch repulsive Kräfte zwischen realen Teilchen zu berücksichtigen sind, ist eine der grundlegenden Schwierigkeiten bei der theoretischen Beschreibung von Flüssigkeiten.

Die Berechnung von g aus dem zwischenmolekularen Potential kann auf verschiedene Weisen erfolgen. Numerische Verfahren nehmen 1000 Teilchen in einem bestimmten Volumen (je schneller die Computer, desto größer die Zahl), deren Bewegungen verfolgt werden, und simulieren den Rest der Flüssigkeit durch identische Kopien dieses kleinen Behälters, die um ihn herum angebracht werden.
Ein häufig angewendetes Verfahren zur Simulation von Flüssigkeiten ist das Monte-Carlo-Verfahren. Dabei werden die Moleküle um kleine, aber völlig zufällige Strecken "verschoben". Ob die entstandene neue Konfiguration akzeptiert wird, wird dann nach bestimmten Regeln entschieden:

  1. Wenn die potentielle Energie der neuen Konfiguration kleiner ist als die der alten, wird die Konfiguration akzeptiert.
  2. Wenn die potentielle Energie des Systems größer ist als vor der Verschiebung, so wird die neue Konfiguration mit einer Wahrscheinlichkeit akzeptiert, die proportional zu e-ΔEN/kT ist. Wir erkennen hier die Boltzmann-Verteilung der Energie wieder. Hierbei ist ΔEN die Änderung des gesamten potentiellen Energie der N Teilchen.

Man kann zeigen, dass dieses Verfahren im Gleichgewicht für eine beliebige Konfiguration mit der Energie EN eine Wahrscheinlichkeit proportional zu e-ΔEN/kT liefert, im Einklang mit der Boltzmann-Verteilung. In den so erzeugten Konfigurationen werden dann einfach die Abstände aller Paare von Teilchen vermessen und diese über viele Konfigurationen gemittelt.

Ein anderer Ansatz zur Simulation von Flüssigkeitsstrukturen ist die Molekulardynamik. Hierbei berechnet man ausgehend von einer zufälligen Anfangsverteilung die Bahnen aller Teilchen unter dem Einfluss der zwischenmolekularen Potentiale. Dazu werden die Newtonschen Bewegungsgleichungen in kleinen Zeitschritten (etwa 10-15s, kürzer als das mittlere Intervall zwischen zwei Stößen) numerisch integriert. Eine Berechnung wird für Tausende derartiger Zeitschritte durchgeführt, und für jede dabei durchlaufende Konfiguration werden die Abstände zwischen den Teilchen ausgewertet.

Aus der radialen Verteilungsfunktion können wir die thermodynamischen Eigenschaften der Flüssigkeit berechnen. Beispielsweise ist der Beitrag der Paarwechselwirkungen zur Inneren Energie durch das Integral

gegeben. Das bedeutet, der Beitrag  ist gleich der mittleren Wechselwirkung Ew zweier Teilchen, gewichtet mit einem Faktor g(r)r2dr, der die Wahrscheinlichkeit angibt, mit der ein Abstand zwischen r und r+dr auftritt. Entsprechend ist der Beitrag der Paarwechselwirkungen zum Druck durch

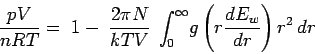
gegeben. Die Größe r · dEW/dr wird als Virial bezeichnet, die angegebene Gleichung daher auch als Virialzustandsgleichung.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.