Wir werden nun untersuchen, welche Konsequenzen sich daraus ergeben, dass dU ein totales Differential ist. Dazu halten wir zunächst fest, dass für ein geschlossenes System konstanter Zusammensetzung U eine Funktion von Volumen und Temperatur ist. Grundsätzlich ist U eine Funktion von V, T und p; diese Größen sind jedoch nicht unabhängig, sondern durch die Zustandsgleichung miteinander verknüpft. Wenn wir V und T vorgeben, ist p somit ebenfalls bestimmt. Für unsere Zwecke ist die Wahl von V und T als Variable am günstigsten, wir könnten aber ebenso p, T oder p, V als unabhängige Zustandsvariable wählen.
Nun wollen wir annehmen, dass sich sowohl V als auch T in infinitesimalen
Schritten ändern und erhalten für die infinitesimale Änderung
der Inneren Energie :
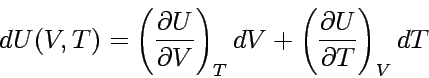 |
In einem geschlossenen System mit konstanter Zusammensetzung ist jede infinitesimale Änderung der Inneren Energie den jeweiligen Änderungen von Volumen und Temperatur proportional. Die Proportionalitätsfaktoren sind dabei die partiellen Ableitungen nach den Zustandsvariablen, hier V und T.
Allgemein ist eine partielle Ableitung die Steigung des Graphen einer
interessierenden Größe in Abhängigkeit von einer
Variabeln, mit der diese Größe in funktionellem Zusammenhang
steht; alle anderen Variabeln werden konstant gehalten. Diese Steigung
kann man in vielen Fällen direkt physikalisch interpretieren. In diesem
Fall ist der Differentialquotient 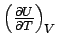 die Wärmekapazität:
die Wärmekapazität:
|
Dies sehen wir, wenn wir uns erinnern,
dass dU = dq - pdV ist, denn daraus folgt: 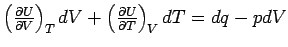 oder nach Umformung oder nach Umformung 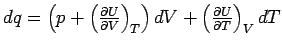 und bei konstantem Volumen (dV = 0) wird daraus
und bei konstantem Volumen (dV = 0) wird daraus
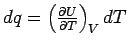 ,
was nichts anderes als unsere Beziehung zwischen
Temperatur und Wärme, nämlich die Wärmekapazität,
ist. ,
was nichts anderes als unsere Beziehung zwischen
Temperatur und Wärme, nämlich die Wärmekapazität,
ist.
|
|
|
Der Koeffizient 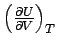 , hat ebenfalls eine wichtige thermodynamische Bedeutung: Er ist ein Maß
für die Änderung der Inneren Energie eines Stoffes, wenn sich
sein Volumen bei konstanter Temperatur ändert. Wir bezeichnen ihn
mit πT, da er die Dimension eines
Drucks besitzt. , hat ebenfalls eine wichtige thermodynamische Bedeutung: Er ist ein Maß
für die Änderung der Inneren Energie eines Stoffes, wenn sich
sein Volumen bei konstanter Temperatur ändert. Wir bezeichnen ihn
mit πT, da er die Dimension eines
Drucks besitzt. |
Damit ist
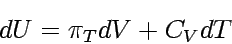 |
Wenn bei der isothermen Expansion einer Substanz (dV > 0) ihre Innere Energie wächst (dU > 0) - dies ist der Fall, wenn zwischen Teilchen Anziehungskräfte wirken - hat der Graph der Inneren Energie in Abhängigkeit vom Volumen eine positive Steigung, es gilt πT > 0. Wenn zwischen den Teilchen keinerlei Wechselwirkung vorhanden ist, hängt die Innere Energie nicht vom gegenseitigen Abstand der Teilchen und daher auch nicht vom Volumen der Probe ab; für ein ideales Gas ist demzufolge πT = 0. Diese letzte Gleichung, d.h., die Feststellung, dass Volumen und Innere Energie voneinander unabhängig sind, ist eine Definition des idealen Gases; sie ist gleichwertig mit der Zustandsgleichung pV = nRT.
Da für ein ideales Gas U = 3/2
RT gilt, d.h. U hängt nicht von V ab, muss 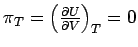 sein. Für CV,m eines idelaen Gases erhalten wir:
sein. Für CV,m eines idelaen Gases erhalten wir:
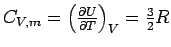 .
.
Partielle Ableitungen haben viele nützliche Eigenschaften. Durch zweckmäßige Verwendung der partiellen Differentialquotienten kann man unbekannte Größen oft in bekannte, interpretierbare oder meßbare umformen. Wie ändert sich z.B. die Innere Energie in Abhängigkeit von der Temperatur bei konstantem Druck des Systems?
Aus der Gleichung 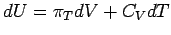 folgt:
folgt:
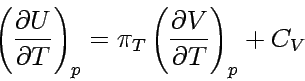
Der Differentialquotient auf der rechten Seite der Gleichung ist die Steigung des Graphen der Funktion V(T) bei konstantem Druck. Diesen Wert findet man tabelliert als Koeffizient der thermischen Ausdehnung α eines Stoffes, er ist definiert als
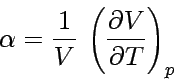
Durch Einsetzen der allgemeinen Definitionsgleichung für α in die Beziehung für 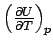 erhält man
erhält man
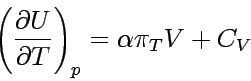 .
.Dies ist eine allgemeine Gleichung für geschlossene Systeme konstanter
Zusammensetzung. Sie beschreibt die Abhängigkeit der Inneren Energie
von der Temperatur bei konstantem Druck als Funktion von CV
(experimentell meßbar), α (durch eine
weitere Messung erhältlich) und 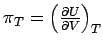 .
Für ein ideales Gas ist πT = 0 und damit
.
Für ein ideales Gas ist πT = 0 und damit
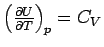 (ideales Gas).
(ideales Gas).Man beachte dabei, dass die Gleichung nur im Spezialfall des idealen
Gases gilt, während
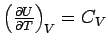 als Definition der Wärmekapazität immer gelten muss!
als Definition der Wärmekapazität immer gelten muss!
Bis zum Ende dieses Kapitels werden wir uns mit einem idealen Gas beschäftigen, dessen Wärmekapazität nicht von der Temperatur abhängt. Durch die Beschränkung auf ein ideales Gas, πT = 0, erhalten wir dU = CVdT. Da für eine adiabatische Expansion/Kompression dq = 0 gelten muss, folgt daraus dU = dw und daher:
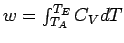
Jetzt nehmen wir noch die Bedingung hinzu, dass die Wärmekapazität temperaturunabhängig sein soll; so ergibt sich
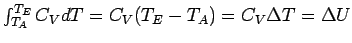
Die Arbeit bei der adiabatischen Volumenänderung eines idealen Gases ist danach proportional zur Temperaturdifferenz zwischen Anfangs- und Endzustand.
Generell kann man aus der letzten Gleichung folgern, dass für
w < 0 (d.h., das System verrichtet Arbeit) ΔT < 0 gilt.
Das überrascht nicht: Da keine Wärme in das System hineingelangen
kann, muss seine Innere Energie abnehmen, wenn das System Arbeit verrichtet.
Die Innere Energie eines idealen Gases wird aber nicht von Volumenänderungen
beeinflußt; daher muss, wenn die Innere Energie abnimmt, die
Temperatur fallen.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.