Wir untersuchen nun die Möglichkeiten, das Gleichgewicht einer
chemischen Reaktion durch Änderung der Reaktionsbedingungen zu kontrollieren.
Die Gleichgewichtskonstante einer Reaktion wird durch Katalysatoren oder
Enzyme (Biokatalysatoren) nicht beeinflußt: Katalysatoren
verkürzen die Zeit zur Einstellung des Gleichgewichts, verändern
aber dessen Lage nicht. Allerdings wird bei industriellen Reaktionen
das Gleichgewicht selten wirklich erreicht, so dass unter diesen Nichtgleichgewichtsbedingungen
Katalysatoren mitunter unerwartete Wirkungen zeigen können und sogar
die Zusammensetzung des Reaktionsgemisches verändern.
Einfluß des Druckes auf das Gleichgewicht
Der Wert der Gleichgewichtskonstanten K hängt vom Wert von ΔrG° ab; letzterer ist definiert bei einem bestimmten Druck, dem Standarddruck p°. Der Wert von ΔrG° (und damit auch der von K) ist daher konstant - unabhängig davon, bei welchem Druck des Systems sich das Gleichgewicht eingestellt hat. Wir schreiben formal für diese Unabhängigkeit:
(∂K/∂p)T = 0.
Daraus, dass K nicht vom Druck abhängt, dürfen wir aber
keinesfalls schließen, dass die Zusammensetzung des Systems
im Gleichgewicht nicht vom Druck beeinflußt wird. Zunächst wollen
wir zwei Arten der Druckausübung unterscheiden. Ein Druck kann dadurch
ausgeübt werden, dass ein Inertgas in das Reaktionsgefäß
gepreßt wird. Wenn sich alle beteiligten Gase ideal verhalten, werden
ihre Partialdrücke durch diesen Vorgang nicht geändert und die
Konzentrationen der reagierenden Gase ändern sich nicht. Es erfolgt
keinerlei Einfluß auf die Zusammensetzung des Systems im Gleichgewicht.
Bei der Kompression hingegen wird das den Gasen zur Verfügung
stehende Volumen verkleinert. Nun ändern sich die Partialdrücke
der reagierenden Gase und damit ihre Konzentraationen. Die Vorgänge
bei der Kompression wollen wir genauer untersuchen, um zu verstehen, wie
sich die Änderung der Partialdrücke mit der allgemeinen Aussage,
K ist unabhängig vom Druck, vereinbaren läßt. Betrachten
wir hierzu beispielsweise das Gleichgewicht A ↔
2B zweier idealer Gase; die Gleichgewichtskonstante ist hierfür
K = pB²/pA
(z.B. N2O4→ 2NO2). Damit die rechte Seite konstant bleibt, muss eine Zunahme von pA genau einer Zunahme des Quadrats von pB entsprechen. Diese gegenüber pB deutlich stärkere Zunahme von pA wird nur erreicht, wenn die Konzentration von B im Gleichgewicht zugunsten der von A abnimmt. Die Anzahl der Moleküle von A nimmt auf diese Weise zu, wenn das Gefäßvolumen verringert wird, und der Partialdruck von A wächst stärker, als durch diese Volumenabnahme allein zu erwarten wäre. Diese Zunahme der Menge von A auf Kosten der Menge von B infolge einer Kompression des Systems ist ein spezieller Fall einer allgemeinen Gesetzmäßigkeit, die von dem französischen Chemiker Henri Le Chatelier vorgeschlagen wurde:
Für die Gleichgewichtskonstante erhält man danach
δ = (1 + 4p/K p°)-½
Aus diesem Ausdruck erkennt man, dass sich - auch wenn K selbst nicht vom Druck abhängt - die Stoffmengen von N2O4 beziehungsweise NO2 sehr wohl in Abhängigkeit vom Druck ändern. Weiterhin sieht man, dass - in Übereinstimmung mit dem Prinzip von Le Chatelier - der Dissozitationsgrad δ abnimmt, wenn p zunimmt.
Zum Schluß eine Randbemerkung zu (∂K/∂p) = 0: Falls wir nicht von Gasreaktionen ausgehen, dann gilt für die Druckabhängigkeit von K:
(∂ ln K/∂p)T = −1/RT(∂ΔG°/∂p)T,
wofür sich, wenn der Standardzustand nicht - wie bei Gasreaktionen
- auf einen Standarddruck bezogen ist, unter Berücksichtigung der
Maxwellschen Beziehung (∂G/∂p)T
= V, weiterhin ergibt
| (∂ ln K/∂p)T = −1/RT ΔV°. |
Dabei bedeutet ΔV° die Volumenänderung
pro Formelumsatz, wenn die Ausgangstoffe aus den Standardzuständen
heraus in die Produkte in Standardzustände überführt werden.
ΔV°
dürfte bei Reaktionen zwischen kondensierten Stoffen in der Größenordnung
von 10-6 m3mol-1 liegen. Bei Raumtemperatur
beträgt RT (T = 300 K) etwa 2,5 ·
103 J mol-1. Damit ist 1/RTΔV°
in der Größenordnung von 10-9 m3J-1
= 10-9 Pa-1 entsprechend 10-4 bar-1.
Das bedeutet, dass sich bei einer Druckänderung um 1 bar
ln K um 0,01% ändert. wir können deshalb bei Reaktionen zwischen
kondensierten Stoffen die Druckabhängigkeit der Gleichgewichtskonstanten
vernachlässigen.
Einfluß der Temperatur auf das Gleichgewicht
Nach dem Prinzip von Le Chatelier ist zu erwarten, dass bei Erhöhung der Temperatur eine endotherme Reaktion begünstigt wird, weil das System dabei Wärme aufnimmt. Analog begünstigt eine Temperaturabnahme die exotherme Reaktion; diese setzt Wärme frei und wirkt somit der Abkühlung des Systems entgegen.
Exotherme Reaktion: Eine Temperaturerhöhung verschiebt das
Gleichgweicht zugunsten der Edukte.
Endotherme Reaktion: Eine Temperaturerhöhung verschiebt
das Gleichgewicht zugunsten der Produkte.
Der Einfluß der Temperatur auf das chemische Gleichgewicht kann über die Gibbs-Helmholtz-Gleichung
d(ΔrG°/T)/dT = -ΔrH°/T2
berechnet werden, wenn wir für ΔrG°
= -RT ln K einsetzten. Wir erhalten dann die van't
Hoff-Gleichung:
| d ln K/dT = ΔrH°/RT² |
Da d(1/T)/dT
= -1/T² ist, können
wir der van't Hoffschen Gleichung auch eine andere Form geben:
| d ln K/d(1/T) = −ΔrH°/R |
Die erste Form der van't Hoffschen Reaktionsisobare, wie auch die Gleichung häufig genannt wird, sagt aus, dass d ln K / dT < 0 für alle exothermen Reaktionen (ΔrH° < 0) ist. Eine negative Steigung bedeutet eine Abnahme von ln K (und daher auch von K) bei steigender Temperatur, d.h. die Lage des Gleichgewichts einer exothermen Raektion wird zugunsten der Ausgangsstoffe verschoben. Für endotherme Reaktionen (ΔrH° > 0) gilt das Gegenteil.
Zum besseren Verständnis dieser Zusammenhänge betrachten wir noch einmal den Ausdruck ΔrG = ΔrH - T ΔrS in der Form -ΔrG / T = -ΔrH / T + ΔrS. Bei einer exothermen Reaktion entspricht -ΔrH/T einer Entropiezunahme der Umgebung, ist also die Treibkraft für die Produktbildung. Bei steigender Temperatur wird der Betrag von -ΔrH/T kleiner; die Entropiezunahme der Umgebung und damit auch die Triebkraft der Reraktion nimmt ab, der Produktanteil im Gleichgewicht wird geringer. Verläuft die Reaktion hingegen endotherm, liegt die Triebkraft vorwiegend in der Entropiezunahme des Reaktionssystems selbst. Der ungünstige Einfluß der gleichzeitigen Entropieabnahme der Umgebung wird bei Anstieg der Temperatur etwas gemildert (da der Betrag von ΔrH/T kleiner wird, so dass die Produktbildung begünstigt wird.
Integration der van't Hoffschen Gleichung
Um den Wert der Gleichgewichtskonstanten bei einer Temperatur T ausgehend von ihrem Wert bei einer anderen Temperatur TA zu bestimmen, müssen wir die van't Hoffsche Gleichung integrieren
Die linke Seite ergibt (ln K2 −
ln K1). Unter der Annahme, dass ΔrH°
im betrachteten Temperaturbereich nicht (oder nur schwach) von T abhängt,
können wir diese Größe vor das Integral ziehen und wir
erhalten das unbestimmte Integral ln K = - ΔrH°/RT
+ Integrationskonstante. Oder für das bestimmte Integral:
| ln K2 = ln K1 −ΔrH°/R (1/T−1/TA) |
| K(T) = K(TA) · exp [− ΔrH°/R (1/T−1/TA)] |
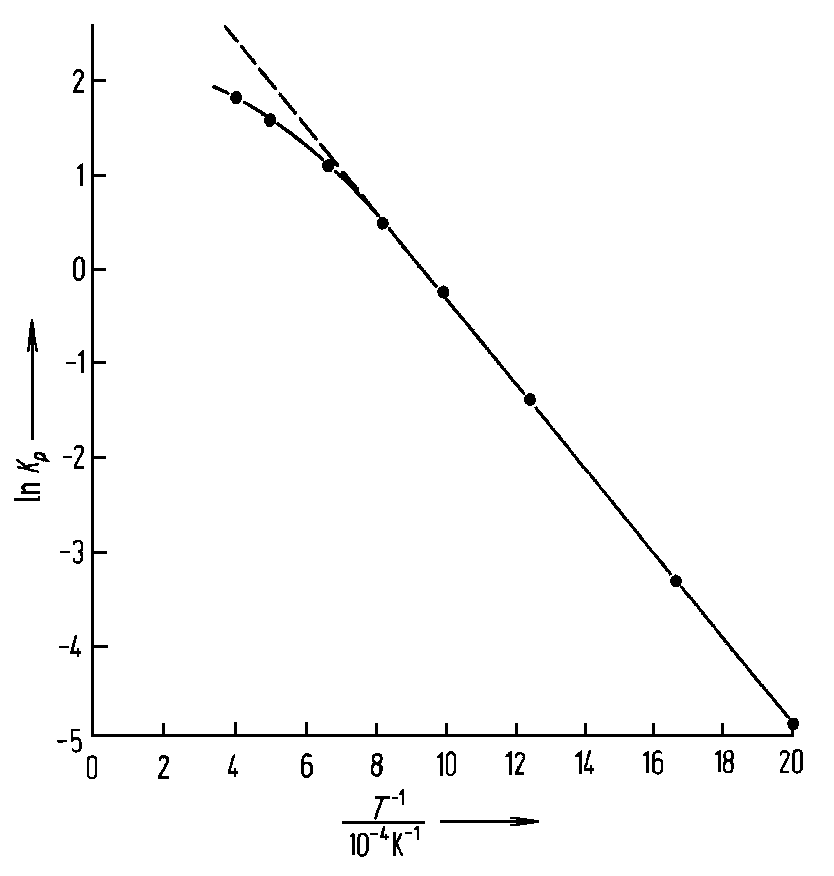 |
| Abb. 1: Temperaturabhängigkeit der Gleichgewichtskonstante Kp für das Wassergas-Gleichgewicht; H2 + CO2↔ H2O + CO. |
ln Kp gegen 1/T
aufgetragen. Man erkennt, dass zwischen 8,3·10-4
K-1
<1/T
<20·10-4
K-1,
entsprechend
ΔHT°
= ΔHT=0°
+ 0∫TΔCp°
dT
ΔH°(T2)
= ΔH°(T1)
+ T1∫T2ΔCp°dT
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.