Siedepunkterhöhung - Gefrierpunkterniedrigung

Den Einfluss eines gelösten Stoffes B im Lösungsmittel A hatten
wir bereits kurz kennengelernt und konnten es qualitativ anhand des chemischen
Potentials verstehen (s. Abb).
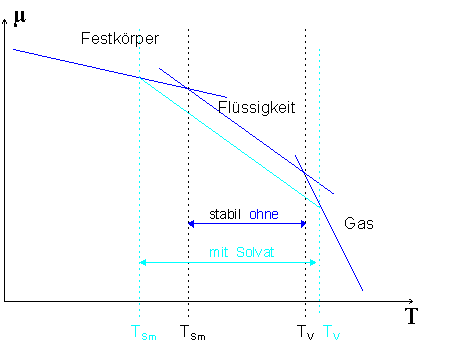 |
| Abb.1:
Prinzipieller Verlauf des chemischen Potentials µ für drei Phasen.
Die Steigung ist durch -Sm
gegeben. Mit Solvat verschiebt sich µ(l) zu niedrigeren Werten
mit entsprechender Änderung des Schmelzpunktes TSm
und des Siedepunktes TV. |
Der Schmelz- (Siede-) Punkt ist durch den Schnittpunkt der jeweiligen chemischen
Potentiale gegeben, d.h. µ(s)=µ(l) für den
Schmelzpunkt und µ(l)=µ(g) für den Siedepunkt.
Das chemische Potential der Flüssigkeit µ(l) verschiebt
sich (zu kleineren Werten) und wir erwarten (s. Abb.) einen geringeren
Schmelzpunkt TSm und einen höheren Siedepunkt TV.
Da die Steigung von µ(s) geringer ist als die von µ(g), erwarten
wir außerdem, dass die Temperaturabsenkung des Schmelzpunktes
größer sein wird als die Erhöhung des Siedepunktes durch
irgendwelche Verunreinigungen. Wir wollen diesen Zusammenhang nun quantitativ
fassen.
Das Gleichgewicht für das Lösungsmittel A wird bei einer
Temperatur T durch
µA(g) = µA*(l)
+ RT ln xA
beschrieben. Diese Gleichung können wir umformen zu:
ln xA = (µA(g)-µA*(l)
)/RT = ΔVGm/RT
wobei ΔVGm die molare
Freie Verdampfungsenthalpie ist. Es interessiert uns die Abhängigkeit
der Temperatur vom Anteil des gelösten Stoffes B. Hierzu müssen
wir zunächst wissen, wie ΔVGm
von der Temperatur abhängt, was über die Gibbs-Helmholtz-Gleichung,{∂(G/T)/∂T}p
= − H/T2,
gelingt:
Differenzieren der obigen Gleichung für ln xA nach
T liefert:
∂ ln xA
/∂T = ∂(ΔVGm
/ RT)/∂T = −ΔVHm/RT²
Integrieren (von T* nach T) und Ersetzen von xA durch
xA = 1-xB ergibt:
ln(1-xB) = ΔVHm/R
[1/T-1/T*]
Da nur kleinere Mengen von B gelöst sind, d.h. der Molenbruch xB klein
ist, kann für den ln näherungsweise geschtieben werden
ln(1-xB)
= -xB. Weiterhin gilt für kleinere Temperaturdifferenzen
ΔT =
T-T*: [1/T-1/T*]
= -(T-T*)/TT*
= -ΔT/T*2. Damit
erhalten wir für die Temperaturerhöhung:
Häufig führt man die ebullioskopische Konstante Keb
des Lösungsmittel ein und drückt ΔT in
Abhängigkeit von der Molalität mB aus:
| Siedepunkterhöhung: ΔT
= Keb mB |
Analog geht man vor, um die Gefrierpunkterniedrigung ΔT =
T*-T zu erhalten (man beachte die "umgekehrte"
Temperaturdifferenz). Wir erhalten dann
mit ΔSmHm als molarer
Schmelzenthalpie. Auch hier führt man die kryoskopische Konstante
KKr ein und drückt ΔT in Abhängigkeit
von der Molalität mB aus:
| Gefrierpunkterhöhung: ΔT
= KKr mB |

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.

![]()