Wir wenden uns jetzt der Diskussion zeitabhängiger Diffusionsprozesse zu, d.h. wir sind daran interessiert, wie sich eine Inhomogenität zeitlich entwickelt. Ein Beispiel hiefür ist das Platzen einer Stinkbombe im Hörsaal und die Ausbreitung des geruchsintensiven Gases im Verlauf der Zeit. Ein anderes Beispiel (mit größerer chemischer Bedeutung) ist die Konzentrationsverteilung einer Lösung, der ein Elektrolyt zugegeben wird. Wir wollen hier die Diffusion von Teilchen untersuchen, ähnliche Argumente gelten jedoch auch für die Diffusion der Temperatur oder anderer physikalischer Eigenschaften.
Die zentrale Gleichung, die die Veränderung der Konzentration eines Stoffes in einem inhomogenen Bereich der Lösung beschreibt, ist die Diffusionsgleichung, welche die Geschwindigkeit, mit der sich die Konzentration eines gelösten Stoffes an einem bestimmten Punkt x einer Lösung verändert, zu der räumlichen Variation der Konzentration an diesem Punkt in Beziehung setzt.
.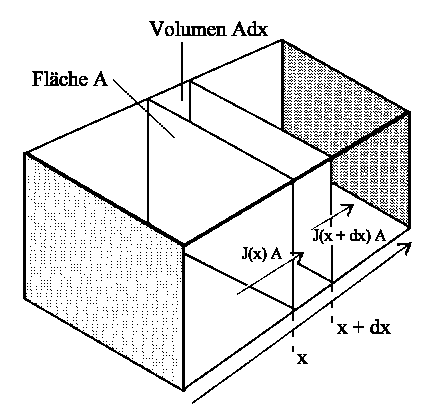 |
| Abb. 1: Der Nettofluss in ein Gebiet ist die Differenz des aus einem Gebiet großer Konzentration (links) eintretenden Flusses und des in die Region kleiner Konzentration (rechts) austretenden Flusses. |
Die zeitliche Änderung wird durch ∂c/∂t beschrieben. Anhand der Abbildung können wir uns klar machen, dass diese zeitliche Änderung über den Zustrom in das Volumen A · dx abzüglich des Abflusses aus diesem Volumen gegeben ist. Die Anzahl N der Moleküle, die pro Zeit in das Volumen einströmen ist über den Strom J(x) = N/ADt gegeben: N/Dt = A · J(x). Entsprechend ist die Anzahl der pro Zeiteinheit abfließenden Moleküle durch N'/Dt = A · J(x + dx) gegeben. Die Konzentrationsänderung (Zahl der Teilchen pro Volumen und Zeit: Dc/Dt = D(N/V)/Dt, V=A·Dx) ist dann
Dc/Dt = (N - N')/ADxDt = [J(x) - J(x+Dx)]/Dx
Da J(x+dx) = J(x) + (∂J/∂x)dx
gilt, erhalten wir ∂c/∂t
= - ∂J/∂x
oder mit dem 1. Fickschen Gesetz J = -D(∂c/∂x):
| ∂c/∂t = D (∂²c/∂x²) |
wobei wir D als ortsunabhängig angenommen haben. Dies ist das 2.
Ficksche Gesetz der Diffusion.
Lösungen der Diffusionsgleichung
Die Diffusionsgleichung ist eine Differentialgleichung zweiter Ordnung bzgl. des Ortes und erster Ordnung bzgl. der Zeit. Um sie zu lösen, müssen wir daher zwei Randbedingungen für die räumliche Variable und eine Anfangsbedingung für die Zeit angeben.
Als Bespiel betrachten wir das Einbringen einer sehr dünnen Schicht
dx von Teilchen zur Zeit t = 0. Diese Randbedingung für die Zeit lautet
also, dass sich für t = 0 alle N0 Teilchen innerhalb
einer Fläche A in der yz-Ebene (bei x = 0) befinden.
Eine Lösung der Gleichung ist:
Welche Grenz- und Ausgangsbedingungen entspricht diese Lösung? Für t → 0 ist c(x,t=0) = 0 für alle Werte von x, ausgenommen x = 0; hierfür ist c →∞ . Diese Situation nennt man eine momentane ebene Quelle am Ursprung. Die Konstante α bezieht sich auf die Stärke der Quelle, also auf die Menge No von Teilchen, die ursprünglich an der Stelle x = 0 vorhanden ist. Wegen der Erhaltung der Teichenzahl muss für eine beliebige Zeit t gelten:
No = A -∞∫+∞ cdx = α-∞∫+∞ t-½ exp(-x2/4Dt) dx = 2αA (πD)½
Ersetzen von α in der Gleichung für
c(x,t) ergibt:
| c(x,t) = No/2A(πDt)½· exp(- x²/4Dt) |
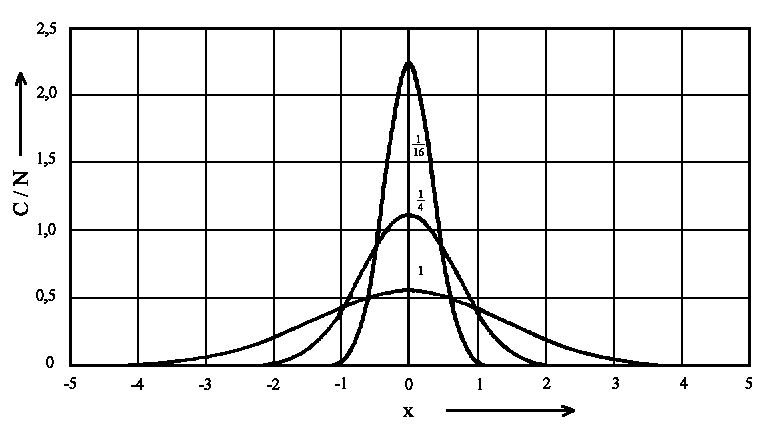 |
| Abb. 2: Konzentrationsprofile für die Diffusion von einer momentanen ebenen Quelle. Die Zahlen an den Kurven bedeuten verscheidene Werte von Δt. |
Die Abbildung zeigt die Funktion für drei verschiedene Werte von Dt; dies demonstriert deutlich, wie sich die Moleküle von der ebenen Quelle aus durch Diffusion ausbreiten.
Ein weiteres nützliches Beispiel ist die Lösung für die
an einem Punkt lokalisierte Konzentration eines gelösten Stoffes in
einem dreidimensionalen Behälter mit Lösungsmittel (einem Stück
Würfelzucker in einem sehr großen Behälter mit Wasser).
Die Konzentration des gelösten Stoffes ist hierbei sphärisch
symmetrisch um den Ausgangspunkt verteilt, die Verteilung lautet
|
|
Bei anderen chemisch und physikalisch interessanten Anordnungen sind Lösungen jedoch komplizierter.
Die Lösungen der Diffusionsgleichung können uns helfen, Diffusionskoeffizienten experimentell zu bestimmen. Bei der Kapillarmethode wird eine dünne, mit einer Lösung des zu untersuchenden Stoffes gefüllte Kapillare, die am oberen Ende verschlossen ist, in einen gut durchmischten Behälter mit Lösungsmittel eingetaucht. Die Substanz diffundiert in das Lösungsmittel, wo ihre Konzentration zu verschiedenen Zeiten bestimmt wird. Zur Auswertung des Experiments löst man die Diffusionsgleichung für dieses System (mit den korrekten Randbedingungen) und kann so den Diffusionskoeffizienten berechnen.
Für den in der Abbildung gezeigten Diffusionsvorgang gibt es eine interessante und wichtige Bedeutungsweise. Wir können nämlich unsere Aufmerksamkeit auf ein individuelles Molekül richten und nach der Wahrscheinlichkeit fragen, mit der es innerhalb einer Zeit t eine Strecke x durch Diffusion zurückgelegt hat. Hierbei müssen wir natürlich einen bestimmten Ausgangsbereich zulassen; wir nennen also p(x)dx die Wahrscheinlichkeit, dass die Moleküle bis in einen Bereich zwischen x und x+dx diffundiert sind. Diese Wahrscheinlichkeit ergibt sich einfach aus der Menge an Substanz zwischen x und x+dx, dividiert durch die gesamte Substanzmenge in der ursprünglichen Quelle. Es ist also:
p(x)dx = C(x)Adx/N0 = 1/2(πDt)½· exp(-x²/4Dt)dx
Unter Berücksichtigung dieser Interpretation können wir nun nach dem mittleren Abstandsquadrat <x2> fragen, das ein Molekül im Zeitraum t durch Diffusion zurückgelegt hat. (Wir können hier nicht einfach <x> verwenden, da die Diffusion in positiver oder negativer Richtung gleich wahrscheinlich ist und daher <x> = 0.) Es ist:
<x²> = -∞∫+∞ x²p(x) dx
| <x²> = 2Dt |
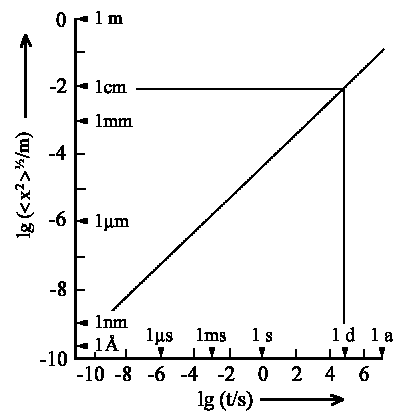 |
| Abb. 3: Der von Teilchen mit D = 5 · 10-10 m2s-1 zurückgelegte quadratisch gemittelte Abstand. Die Diffuion ist ein sehr langsamer Prozeß. |
Diese einfache Beziehung wird sehr oft für die rasche Abschätzung mittlerer Diffusionsabstände verwendet, und zwar nicht nur in Gasen, sondern auch in Flüssigkeiten und Festkörpern. Geologen beschäftigen sich z.B. mit der Frage, ob Diffusion im festen Zustand ein Mechanismus für den Transport mineralischer Bestandteile sein könnte. Ein recht typischer Diffusionskoeffizient für einen Diffusionsvorgang im festen Zustand bei Umgebungstemperatur ist der für Helium in Turmalin: 10-8 cm2s-1. Wie weit würde nun ein Heliumatom in einem Turmalinkristall in einer Million Jahren ( = 3,156 · 107 Sekunden) diffundieren?
<x²> = 2 · 10-8 · 106. 3,156 · 107 = 6,212 · 105 cm2
(<x²>)½ = 788 cm
Solche Zahlen sind auch für kosmische Forschungen von großer
Bedeutung, etwa bei der Frage nach dem Alter von Meteoriten und der Auswirkung
kosmischer Strahlung auf Mineralien.
Für Teilchen mit einem typischen Diffusionskoeffizienten (D =
5 · 10-10 m2s-1 in Flüssigkeiten)
ist (<x2>)½
in der Abbildung aufgetragen. Wir können daraus ablesen, wie lange
ein Teilchen etwa braucht, um eine bestimmte Strecke durch Diffusion zurückzulegen.
Die beiden eingezeichneten Linien zeigen, dass es ungefähr einen
Tag benötigt, um eine Strecke von 1 cm zurückzulegen. Die Diffusion
ist offensichtlich ein sehr langsamer Prozess (weswegen man Lösungen
meist rührt, um die Durchmischung durch Konvektion
anstatt durch Diffusion zu erreichen).
Wenn wir uns die Diffusion anschaulich vorstellen, so denken wir an
einen völlig betrunkenen Menschen, der sich mit kleinen, zufälligen
Schritten an einer Wand entlang bewegt (also mal vor, mal wieder zurück)
und sich von seinem Ausgangspunkt entfernt. Wir nehmen an, dass unser
Zecher in einer Zeit τ einen Schritt der Länge
s ausführen kann. Er legt daher in der Zeit t eine Entfernung t .
s/τ
zurück. Er muss sich jedoch keineswegs in der Entfernung vom
Ausgangspunkt befinden, da die einzelnen Schritte in zufällige Richtungen
erfolgen (schließlich ist der freie Wille bei genügendem
Alkoholgenuss
ausgeschaltet). Wir vereinfachen unser Modell, indem wir annehmen, dass
alle Schritte die gleiche Länge s haben sollen. Auf diese Weise repräsentiert
unser Trunkenbold eine eindimensionale ungeordnete Bewegung. Eine statistische
Analyse dieser ungeordneten Bewegung zeigt, dass die Wahrscheinlichkeit,
den Volltrunkenen oder eben ein Teilchen nach der Zeit t in einer Entfernung
x vom Ursprung anzutreffen, durch
| P = (τ/2πts²)½e-x²τ/2ts² |
ist. Die Gleichung besitzt exakt die gleiche Form wie wir sie von der Diffusion her kennen. Die Tatsache, dass die beiden auf so verschiedenen Wegen erhaltenen Ausdrücke so ähnlich sind, legt die Vermutung nahe, dass wir die Diffusion tatsächlich als Ergebnis sehr vieler kleiner Sprünge in zufällige Richtungen betrachten können.
Wir können den Diffusionskoeffizienten D durch die Schrittweite
s und die Häufigkeit der Schritte ausdrücken. Durch Vergleich
der Exponenten in den beiden Wahrscheinlichkeitsverteilungen erhalten wir
die Einstein-Smoluchowski-Gleichung:
| D = s²/2τ. |
Wir wollen uns wieder anhand eines typischen Beispiels die beteiligten Größenordnungen klarmachen. Angenommen, ein Ion (z.B. Na+ oder SO22-) springt bei jeder Bewegung in wässriger Lösung ungefähr um seinen eigenen Durchmesser: Mit D = 5 · 10-10 m2s-1 und s = 200pm folgt dann τ = 40ps. Da τ die Zeit für einen Sprung ist, springt das Ion mehr als 1010 mal pro Sekunde (1/τ) ein Stück weiter.
Die Einstein-Smoluckowski-Gleichung ist die entscheidende Verbindung zwischen der mikroskopischen Beschreibung der Bewegung von Teilchen und den makroskopischen Kenngrößen der Diffusion (dem Diffusionskoeffizienten und der Viskosität). Sie schließt außerdem den Kreis, indem sie uns zu den Eigenschaften des idealen Gases zurückführt. Wir können nämlich s/τ als <v>, also als mittlere Geschwindigkeit der Moleküle, interpretieren und s als mittlere freie Weglänge. Damit wird aus der Einstein-Smoluchowski-Gleichung aber genau der Ausdruck, den wir aus der Diffusionsgleichung erhalten haben: D = <v>.s/2 ≡ 1/2<v>λ. Die Diffusion in idealen Gasen ist also nichts weiter als eine ungeordnete Bewegung mit der mittleren freien Weglänge als mittlerer Schrittweite.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.