Reaktion 2. Ordnung

Die Elementarreaktionen 2 A → C + D ist zweiter Ordnung. Ein Beispiel ist der atmosphärische Abbau des OH-Radikals :

OH + OH → H2O + O

oder der Aufbau von Wasserstoffperoxid über das HO2-Radikals :

HO2 + HO2 → H2O2 + O2

Grundsätzlich ist jede Elementarreaktion A + B → C + D zweiter Ordnung. Nur wenn eine Konzentration deutlich größer ist als die andere (z.B. [B] >> [A]), dann wird man im Experiment einen Abbau der geringeren Konzentration ([A]) beobachten, die dem Gesetz erster Ordnung gehorcht (Reaktion Pseudo-erster-Ordnung).

Beispiele für bimolekulare Elementarreaktionen (2. Ordnung) gibt es wie Sand am Meer, da nahezu alle Reaktionen bimolekular ablaufen. Z.B. ist die Elementarreaktion, die das Kohlenmonoxid aus der Atmosphäre entfernt, bimolekular,

CO + OH → CO2 + H,

und gehorcht daher dem Geschwindigkeitsgesetz

- d[CO]/dt  =  k [CO] [OH]

Wenn in der Atmosphäre stetig OH durch andere Prozesse nachgeliefert wird, dann ist [OH] zeitunabhängig und der Abbau des CO erfolgt nach dem Geschwindigkeitsgesetz erster Ordnung:

- d[CO]/dt  =  k' [CO]          mit   k'  = k [OH]

Die Zeit τ bis nur noch 1/e der CO-Ausgangskonzentration vorhanden ist, ist dann τ = 1/k' = 1/k[OH]. Wenn wir wissen, wieviel OH in der Atmosphäre vorhanden ist und wenn wir (im Labor) bestimmen wie groß k ist, dann können wir die Verweildauer des Kohlenmonoxids in der Atmosphäre berechnen.

Doch zurück zur Reaktion 2. Ordnung:
Für die Elementarreaktion 2A → C + D muss natürlich der Abbau von A nach dem Geschwindigkeitsgesetz 2. Ordnung erfolgen. Ebenso muss der Aufbau von C bzw. D nach 2. Ordnung erfolgen. Die Geschwindigkeiten der Konzentrationsänderung, d.h. −d[A]/dt, bzw. d[C]/dt oder d[D]/dt, ist jedoch unterschiedlich, da zwei Teile von A verbraucht werden, um ein Teil C zu bekommen. Daher ist es im Allgemeinen sehr sinnvoll, die Geschwindigkeit einer Reaktion auf den Stoffumsatz zu beziehen, denn dann gilt v = −½d[A]/dt = d[C]/dt = d[D]/dt.

Auch bei zusammengesetzten Reaktionen vom allgemeinen Typus

νAA + νBB →νCC + νDD

gilt dann immer (ν positiv bei Produkten, negativ bei Edukten):
 
v  =  1/νAd[A]/dt  =  1/νBd[B]/dt  =  1/νCd[C]/dt  =  1/νDd[D]/dt

Für unsere Elementarreaktion 2A → C + D ist es daher sinnvoll, die folgende DGL aufzustellen:

−½ d[A]/dt  =  k2 [A]2

Wir können diese natürlich mit 2 multiplizieren und die Konstante k2' = 2 · k2 einführen, um die DGL zu erhalten, die in den meisten Lehrbüchern behandelt wird:

−  d[A]/dt  =  k2' [A]2

Die Lösung der DGL erfolgt nach dem selben Schema:

"Sammeln" gleicher Abhängigkeiten:    [A]o∫[A]  d[A]/[A]²  =  −k2' o∫t dt

Integrieren und Grenzen einsetzen:     −1/[A] + 1/[A]o  =  − k2' t

Auflösen nach [A]:

[A]  =  [A]o/(1 + k2'[A]o t)

oder für unsere bessere DGL:

[A]  =  [A]o/(1 + 2k2[A]o t)

Fragen wir nun nach der Halbwertzeit, d.h. nach der Zeit t½ bei der nur noch die Hälfte der Ausgangssubstanz, [A] = [A]o/2, vorhanden ist, dann ergibt eine einfache Rechnung:
 

t½  =  1/k2'[A]o         bzw.        t½  =  1/2k2[A]o
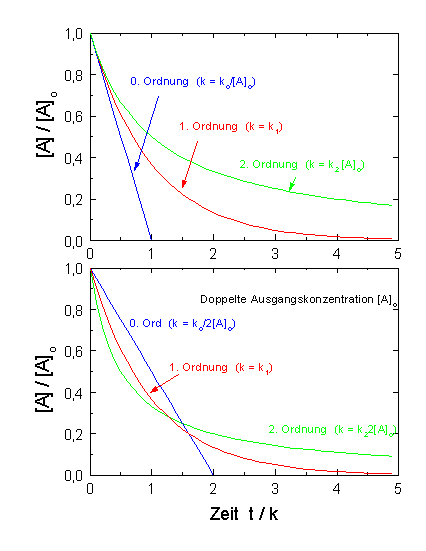Abb.1: Der zeitliche Verlauf einer Reaktion 0., 1., bzw. 2. Ordnung. Im unteren Bild ist die Anfangskonzentration [A]o verdoppelt worden. Nur die Reaktion 1. Ordnung ist unabhängig von [A]o.

Die Halbwertszeit ist also umgekehrt proportional zur Ausgangskonzentration [A]0.
Wir erkennen hier den drastischen Unterschied zu einer Reaktion 1. Ordnung, bei der die Halbwertszeit unabhängig von der Ausgangskonzentration war. In der Abbildung ist der zeitliche Verlauf für eine Reaktion 0., 1. und 2. Ordnung dargestellt. Um einen direkten Vergleich zu ermöglichen, ist im oberen Bild für die Geschwindigkeitskonstante der Reaktion 0. Ordnung k = ko/[A]o, für eine Reaktion 1. Ordnung k = k1 und für eine Reaktion 2. Ordnung k = k2[A]o gesetzt.

Fragen wir nach dem zeitlichen Verlauf der Produktbildung bzgl. C, dann gilt (dank der "besseren" DGL):

− ½ d[A]/dt  =  d[C]/dt  = k2[A]²

Nach Einsetzen der zeitabhängigen Konzentration von A muss die Gleichung nur noch integriert werden:

[C]o∫[C] d[C]  =  k2 [A]o2 o∫t dt / (1 + 2 k2[A]ot)2

[C]  =  k2 [A]o² t/(1 + 2k2 [A]o t)

Schauen wir uns nun die Elementarreaktion A + B → C + D an:

− d[A]/dt  = −d[B]/dt  =  k2 [A] [B]

[A] und [B] sind beide zeitunabhängig, doch nach Einführen der Umsatzvariablen x, die sicherstellt, dass jeweils gleiche Mengen von A und B reagieren müssen, erhalten wir:

[A]  =  [A]0 − x     und     [B]  =  [B]0 − x

Unsere DGL wird damit

dx/dt  =  k2 ([A]o−x)·([B]o−x)
oder
o∫x dx/([A]o−x) ([B]o−x)  =  k2 o∫t dt

Mit Hilfe der Partialbruchzerlegung finden wir

1/[B]o−[A]o.{o∫x  dx/[A]o−x - o∫x  dx/[B]o−x}  =  k2t

− ln([A]o−x) + ln[A]o + ln([B]o−x) - ln[B]o  =  ([B]o− [A]o) k2t

Auflösen nach x führt auf den häßlichen Ausdruck:
 

x  =  [A]o[B]o (e([B]o−[A]o) k2t  − 1 )/([B]o e([B]o−[A]o) k2t  − [A]o)

Insbesondere für [A]o = [B]o sieht es übel aus, da wir dann Null durch Null teilen. Die Regel von l'Hopital bzw. eine einfache Entwicklung der e-Funktion führt uns aber auf das richtige Ergebnis:
 

x  =  [A]o2 k2t / (1 + [A]o k2t)

Wenn wir [A] = [A]o - x einsetzen, erhalten wir

[A]  =  [A]o / (1 + [A]o k2t),

was mit unserem Ergebnis für die Reaktion 2A → Produkte übereinstimmt (bis auf den Faktor 2 beim k2, wg. 2A).

Doch was geschieht, wenn eine Ausgangskonzentration (z.B. [B]0) deutlich größer als die andere Ausgangssubstanz ([A]0) ist ? Die Antwort gibt das Kapitel  Pseudo-erster-Ordnung
 
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.