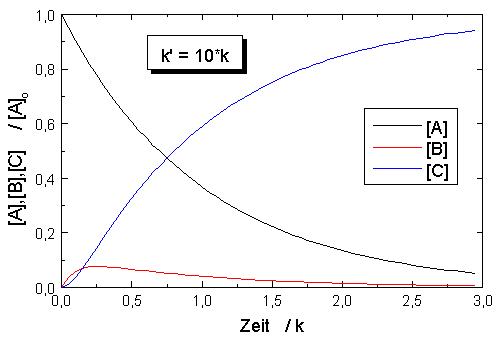
Abb. 1: Zeitlicher Verlauf für den Prozess A → B  → C  mit den Geschwindigkeitskonstanten k und k'. Für ein sehr reaktives Zwischenprodukt [B], d.h. für k' >> k, ist [B] und insbesondere  d[B]/dt sehr klein.

Die Diskussion des zeitlichen Verlaufs von C in der Folgereaktion A → B → C hat ergeben, dass bei zwei Folgereaktionen 1. Ordnung eine Vergrößerung von k' im Verhältnis zu k₁ zwei Effekte hat. Zum einen verringert sich die maximal auftretende Konzentration des Zwischenprodukts, zum anderen verschiebt sich die Lage des Maximums zu kürzeren Zeiten, bezogen auf das Verschwinden des Ausgangsstoffes A.
Wie aus den Abbildungen für die Folgereaktion hervorgeht, ist für k' >> k (s. auch nebenstehende Abb.), also für ein sehr reaktives Zwischenprodukt, [B] stets sehr klein. Auch d[B]/dt hat sehr kleine Werte, wenn man vom Anstieg bis zum Maximum absieht. Dabei ist die Bewertung "klein" nicht absolut, sondern immer im Vergleich zu den Änderungsgeschwindigkeiten der Konzentrationen der übrigen Reaktionsteilnehmer zu sehen. Da das Maximum für sehr großes k' sehr schnell erreicht ist, kann man in guter Näherung für fast die gesamte Reaktionszeit d[B]/dt gegenüber den anderen Umsetzungsgeschwindigkeiten vernachlässigen. d.h.
 

setzten. Dies ist die Quasistationaritätsbedingung, eine Näherung, die die Behandlung - besonders der komplizierten - Geschwindigkeitsgleichungen sehr vereinfacht.
Wenden wir die Quasistationaritätsbedingungen auf das A → B → C - Problem an, so folgt für die Konzentration des Zwischenprodukts B:

Setzen wir diesen Ausdruck in die DGL für C ein, so erhalten wir

und unter Berücksichtigung von [A]

Die Integration ergibt unter Berücksichtigung der Randbedingung [C] = 0 für t = 0

was identisch ist mit der Gleichung, die wir als Näherung der exakten Lösung für k' >> k erhalten haben.
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.