Herleitung der Planckschen Strahlungsformel à la Einstein

Herleitung der Planckschen Strahlungsformel
à la Einstein

Jeder Lichtwelle der Frequenz ν wird eine Anzahl von Photonen zugeordnet. Ferner geht man von der Annahme aus, dass es diskrete atomare (oder molekulare) Energieniveaus gibt.

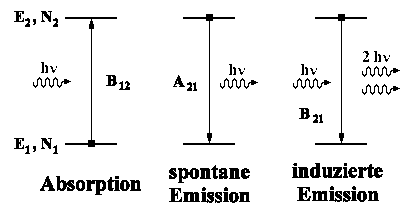hν = E₂ - E₁

Absorption eines Lichtquants hν bringt das Atom oder das Molekül aus dem energetisch tieferen Zustand E₁ in den höheren Zustand E₂. Die Zahl der Absorptionsprozesse je Zeiteinheit ist der Besetzungszahl N₁ (Zahl der Atome/Moleküle im unteren Zustand 1) und der Strahlungsdichte u(ν) proportional. Die Wahrscheinlichkeit für einen solchen Prozess wird mit dem Buchstaben B₁₂ angegeben:

^dN2/_dt = B₁₂ · u(ν) · N₁

Emission eines Lichtquants hν = E₂ − E₁ entspricht einem Übergang vom energetisch höheren zum niedrigeren Zustand. Wie bei der Absorption kann ein solcher Übergang durch Einstrahlen von Photonen erzwungen werden. Bei dieser induzierten Emission erhöht sich die Anzahl der Photonen und die Besetzungszahl N₂ verringert sich pro Zeit um:

^dN2/_dt = - B₂₁ · u(ν) · N₂

spontane Emission erfolgt aus dem Zustand E₂, die Besetzungszahl N₂ verringert sich also:

^dN2/_dt = − A₂₁ N₂

Im Gleichgewicht treten gleich viele Übergänge in beiden Richtungen (Absorption und Emission) auf; also darf sich im Mittel die Besetzungszahl nicht ändern:

^dN2/_dt = 0 (summiert über alle drei Prozesse)

^dN2/_dt = B₁₂ u(ν)N₁ − B₂₁ u(ν)N₂ − A₂₁N₂ = 0

→ B₁₂u(ν)N₁ = (B₂₁u(ν)+A₂₁)N₂

(B₁₂u(ν))/(A₂₁+B₂₁u(ν))	=	N₂/N₁	=	e^−E2^/kT/e^−E1^/kT	=	e^−hν/kT
			→	thermisches Gleichgewicht, daher Boltzmann-Verteilung

u(ν) = A₂₁/(B₁₂ e^hν/kT − B₂₁)

Die Koeffizienten A₁₂, B₁₂ und B₂₁ werden durch die experimentelle Erfahrung bestimmt:

® ¥

B₁₂ = B₂₁

→

u(ν) = (A₂₁/B₁₂)_/(e^hν/kT− 1)

2.) Für kleine Frequenzen, hν << kT, muss das experimentell verifizierte Rayleigh-Jeans-Gesetz {u(ν) = ^8pn²/_c³· kT}
gelten:
Reihenentwicklung: e^h

/kT

» 1 + ^h

^ν

/_kT + .... ® u(

) ≈ A₂₁/B₁₂ ^.kT/_h

_ν

Rayleigh-Jeans-Gesetz

A₂₁/B₁₂ = ^8πhn
³/_c³

Wichtig ist hier der ν³ Zusammenhang zwischen spontaner Emission und Absorption!
Fassen wir alle Informationen über die Koeffizienten B₁₂, B₂₁ und A₂₁ zusammen, dann erhalten wir die Plancksche Strahlungsformel:

u(ν) = ^8π^hν³/_c³^.1/_ehν/kT_−
1

So ganz nebenbei, haben wir auch ein Verständnis über die Wirkungsweise eines Lasers gewonnen; denn wir müssen nur noch die obige Formel {^dN2/_dt = B₁₂ u(ν)N₁ − B₂₁ u(ν)N₂ − A₂₁N₂ } bzgl. des Strahlungsfeldes u(ν) "uminterpretieren":
Wir erhalten dann einen Laser, wenn die Erzeugung der Photonen insgesamt >0 ist. Damit u(ν) zunimmt, muss N₂ abnehmen, d.h. ^dN2/_dt < 0, muss für eine Lasertätigkeit gelten:

B₁₂ u(ν)N₁ − B₂₁ u(ν)N₂ − A₂₁N₂ < 0

oder, unter Vernachlässigung von der spontanen Emission, muss immer gelten

N₂> N₁,

d.h. die Besetzungszahl des oberen (energiereicheren) Niveaus muss größer sein als die des unteren (energieärmeren) Niveaus. Dies ist aber im thermischen Gleichgewicht nicht möglich, wie uns die Boltzmannsche Energieverteilung lehrt. Daher können Laser nur im thermodynamischen Nichtgleichgewicht betrieben werden.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.