Ein Wellenpaket und seine Fourierkomponenten

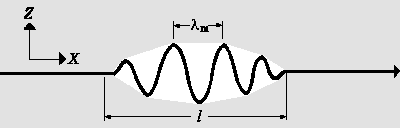Abb.1a: Dieses Wellenpaket kann dadurch gebildet werden, dass eine große Zahl von unendlich langen Sinuswellen, ähnlich den unten gezeigten, einander überlagert werden. (vgl. Kapitel Konstruktion von Wellenpaketen)

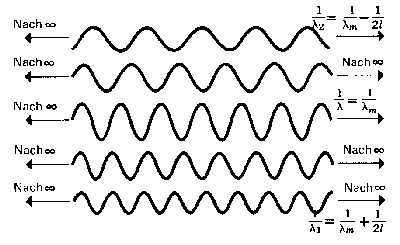Abb.1b: Einige der Fourierkomponenten des Wellenpakets

Eine Möglichkeit, um aus einer Welle ein Teilchen zu machen, ist es, ein Wellenpaket zu konstruieren. Ein Wellenpaket ist eine Welle, die im wesentlichen auf einem Raumbereich der Länge l beschränkt ist, wie in der Abbildung gezeigt wird. Da das Quadrat der Amplitude der Welle in einem Punkt mit der Wahrscheinlichkeit in Zusammenhang steht, das Teilchen an diesem Punkt anzutreffen, gibt es eine große Wahrscheinlichkeit dafür, das Teilchen irgendwo im Inneren dieses Bereichs zu finden, der von dem Wellenpaket eingenommen wird, wogegen die Wahrscheinlichkeit dafür, das Teilchen außerhalb anzutreffen, gleich Null ist. Die möglichen Werte für die x-Koordinate des Teilchens erstrecken sich daher über einen engen Wertbereich der Länge l, und es gilt

Es könnte so aussehen, als ob wir für die Wellenlänge des Wellenpakets die Länge λ_m annehmen könnten, die in der Abbildung eingetragen ist, und dass wir damit dem Impuls des Wellenpakets den genauen Wert

zuschreiben könnten. Jedoch erlaubt uns die strenge mathematische Formulierung der Quantenmechanik eine Beziehung dieser Art nur auf eine unendlich lange Sinuswelle anzuwenden. Glücklicherweise kann das Wellenpaket endlicher Länge durch eine große Anzahl von unendlich langen Sinuswellen unterschiedlicher Wellenlängen dargestellt werden, die den in der unteren Abbildung gezeigten Wellen ähnlich sehen. Diese unterschiedlich langen Sinuswellen verschiedener Wellenlängen werden Fourier-Komponenten des Wellenpakets genannt (Joseph Fourier). Wenn ihre Wellenlängen (oder Frequenzen), Amplituden und Phasen richtig ausgewählt werden, heben sich bei einer Überlagerung aller Fourier-Komponenten die Anteile außerhalb des Wellenpakets gegenseitig vollkommen auf, während sie im Inneren des Wellenpakets die Welle aus der oberen Abbildung ergeben.

Nahezu alle der Fourier-Komponenten besitzen Wellenlängen, die zwischen λ₁ undλ₂ liegen, wobei gilt

Der Wert von λ_m liegt zwischen den Werten λ₁ und λ₂. Die entsprechenden Impulse sind

und

Der Impuls, der dem Wellenpaket zuzuschreiben ist, ist daher keine genau definierte Größe, sondern erstreckt sich über einen Bereich

Aus dieser Gleichung und Δx = l ergibt sich
 

Die Heisenbergsche Unschärferelation ist also ein innerer Bestandteil des Wesens eines derartigen Wellenpakets.

Im Falle eines Elektrons (oder eines beliebigen anderen Teilchens mit einer von Null verschiedenen Ruhemasse) ist jede Fourier-Komponente eine de Broglie-Welle. Die Geschwindigkeit V einer de Broglie-Welle beträgt

Die Gleichung für den Impuls eines Teilchens, p = ^h/_λ, und p = mv beinhalten, dass es für jeden Wert der Wellenlänge λ einer Fourier-Komponente einen entsprechenden Wert der mit ihr verknüpften Geschwindigkeit v des Teilchens gibt. Die Geschwindigkeit V einer Fourier-Komponente ist daher verschieden für Komponenten mit verschiedenen Wellenlängen. Dies ist die Erscheinung der Dispersion, welche dem Verhalten von Licht beim Durchgang durch Glas ähnlich ist. Während sich das Wellenpaket vorwärts bewegt, laufen die verschiedenen Fourier-Komponenten immer mehr auseinander. Obwohl sie anfangs bei einer Überlagerung noch das Wellenpaket aus der oberen Abbildung ergeben, bleibt dies nicht so, wenn die Zeit weiterläuft.
Was dann geschieht, ist in der nebenstehenden Abbildung dargestellt.
 

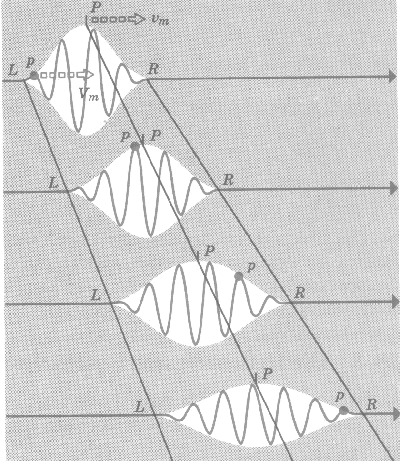Abb. 2: Auseinanderlaufen eines des Broglie-Wellenpakets bei seiner Ausbreitung durch den Raum.

Wenn sich das Wellenpaket vorwärts bewegt, verbreitert es sich ständig. Die Geschwindigkeit seines linken Endes L ist kleiner als die Geschwindigkeit seines rechten Endes R. Dieses hängt mit der Tatsache zusammen, dass die Geschwindigkeit des Teilchens keine genau definierte Größe ist, sondern eine Unschärfe Δv_x besitzt. Die Einhüllende des Wellenpakets wird in der Abbildung als Grenze zwischen dem hellen Wellenpaket und dem dunkleren Untergrund sichtbar, und P ist ihr Maximum. Die Geschwindigkeit von P wird die Gruppengeschwindigkeit genannt, und es kann gezeigt werden, dass sie gleich
 

ist. Die Geschwindigkeit von P ist dasselbe wie die Durchschnittsgeschwindigkeit des Teilchens, was ein vernünftiges Ergebnis ist.

Jetzt können wir die Schwierigkeit auflösen, dass die Geschwindigkeit einer de Broglie-Welle gleich ^c²/_v ist, was nicht gleich v und sogar größer als c ist. Sehen Sie sich die Welle im Inneren der Einhüllenden und den Wellenberg p an, der durch einen dicken Punkt in der Abbildung markiert ist. Dieser Wellenberg p breitet sich nicht mit derselben Geschwindigkeit wie das Maximum der Einhüllenden P aus, sondern mit der größeren Geschwindigkeit

Dieses ist die Geschwindigkeit der Fourier-Komponente mit der Durchschnittswellenlänge λ_m. Sie wird die Phasengeschwindigkeit des Wellenpakets genannt. Der Wellenberg p bewegt sich daher schneller als die Einhüllende vom linken Ende L zum rechten Ende R des Wellenpakets. Es treten also ständig Wellen bei L aus und verschwinden wieder bei R.

Wir brauchen nichts zu befürchten, wenn die Phasengeschwindigkeit V_m größer als c ist. Das Elektron, welches das physikalisch wichtige Gebilde ist, bleibt im Inneren der sich langsam fortbewegenden Einhüllenden, die sich mit der Gruppengeschwindigkeit v_m bewegt, und kann somit niemals eine Geschwindigkeit erreichen, die größer als c ist.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.