Kugeln und Elektronen
A. Wellen
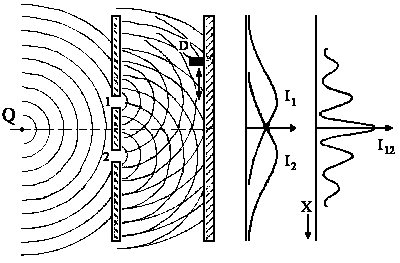 |
| Abb. 1: Beugungsversuch mit Wasserwellen |
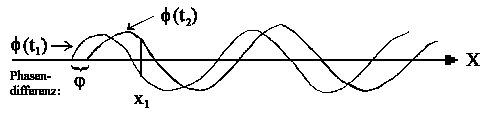 |
| Abb. 2: Verteilung einer Welle f in x-Richtung für zwei Zeiten t1 und t2. |
Zwei Wasserwellen entstehen an den Löchern 1 und 2 und überlagern
sich beim Detektor D zu einer Intensität I. Halten wir ein Loch zu,
dann erhalten wir nur eine Welle: Wir erkennen sofort die sinusförmige
Verteilung der Welle zu einem bestimmten Zeitpunkt t. Der Abstand zwischen
zwei Wellenbergen (oder Tälern) ist dann die Wellenlänge
l. Greifen wir einen beliebigen Punkt x heraus, dann schwingt an
dieser Stelle φ als Funktion von t wiederum
wie eine Sinuswelle, wobei die Wiederholfrequenz durch v beschrieben
wird.
Ein Detektor D registriert die Intensität I der Welle, die durch
I = |φ|2 gegeben ist.
Wir lassen nun beide Löcher offen und beobachten die Überlagerung
der beiden Wellen φ1 und φ2,
die die gleiche Frequenz haben sollen; allerdings können sie um die
Phase j gegeneinander verschoben sein
(s. Abb. 2). Es gilt dann:
|
I = |φ1+φ2|2 |
Eine genauere Auswertung zeigt, dass für die Intensität
gilt: I = I1 + I2 + 2(I1I2)½.cos
j.
Die Intensität schwankt also mit
cos j.
Besonders extrem sind diese Oszillationen für I1
= I2 = I0, denn dann schwankt die Gesamtintensität
zwischen 0 und 4 I0: I = 2I0·(1+cos
j).
D.h. wir erhalten im Extremfall nicht die doppelte, sondern die vierfache
Intensität. Dies gilt natürlich für jeden Punkt x, wobei
die Phase aber auch an jedem Ort x anders ist.
B. Kugeln
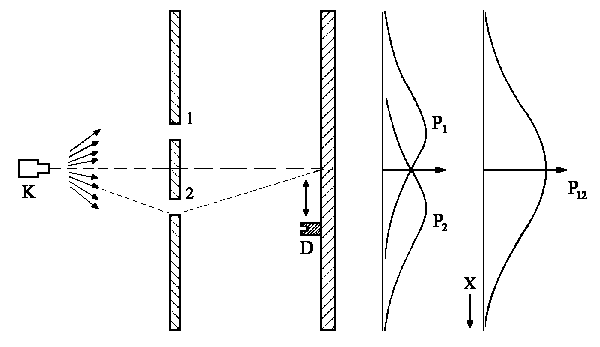 |
| Abb. 3: Streuversuch mit Kugeln eines Maschinengewehrs |
Bei einem „Interferenz“ Experiment mit Kugeln finden wir eine bestimmte
Wahrscheinlichkeitsverteilung P1 für den Durchgang durch
Loch 1, wenn wir Loch 2 zuhalten (bitte nicht mit der Hand) und entsprechend
eine Wahrscheinlichkeitsverteilung P2 für den Durchgang
durch Loch 2, wenn wir Loch 1 zuhalten. Sind beide Löcher geöffnet,
dann finden wir, dass sich die Wahrscheinlichkeit für
den Durchgang durch Loch 1 (P1) und durch Loch 2 (P2)
addieren:
| P12 = P1 + P2 |
 Wenn
die Löcher weit voneinander getrennt sind, dann sind auch die Verteilungen
P1 und P2 getrennt. Hier ist diese Situation etwas
brachialischer dargestellt:
Wenn
die Löcher weit voneinander getrennt sind, dann sind auch die Verteilungen
P1 und P2 getrennt. Hier ist diese Situation etwas
brachialischer dargestellt:
C. Elektronen
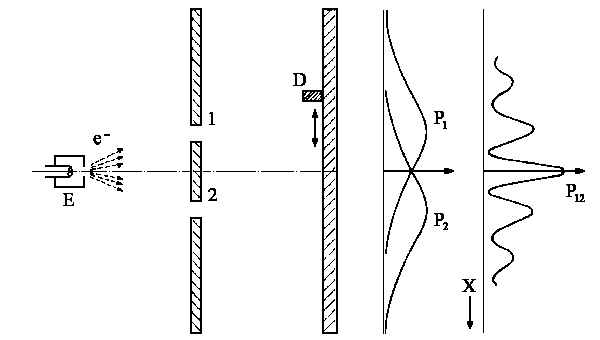 |
| Abb. 4: Man beobachtet P12¹ P1+ P2, auch wenn immer nur ein Elektron nach dem anderen am Detektor ankommt. |
Bei einem vergleichbaren Experiment mit Elektronen stellen wir
fest, dass die Wahrscheinlichkeit P12 nicht die
Summe der Einzelwahrscheinlichkeiten ist und zwar auch dann nicht, wenn
sichergestellt ist, dass immer nur ein Elektron nach dem anderen
am Detektor ankommt.:
| P12 ¹ P1 + P2 |
Was wir als Intensitätsverteilung auf den Schirm beobachten entspricht
genau dem Interferenzverhalten von Wellen, die wir ja inzwischen bestens
beschreiben können (hoffentlich). Danach können wir das Ergebnis
durch zwei komplexe Zahlen φ1
und φ2 beschreiben. Das Absolutquadrat
von φ1 ergibt den Effekt wenn nur
Loch 1 offen ist: P1 = |φ1|2.
Analog für Loch 2 offen (aber Loch 1 geschlossen): P2 =
|φ2|2. Sind aber beide
Löcher offen, dann erhalten wir:
| P12 = |φ1+φ2|2¹ |φ1|2 + |φ2|2 |
Um die Beobachtungen richtig zu beschreiben, müssen wir also mit komplexen Zahlen rechnen. Soweit die Mathe; doch kommt nun das einzelne Elektron durch Loch 1 oder durch Loch 2 ?
Um das herauszufinden, führen wir ein Experiment durch, bei dem
die Elektronen mit Licht beobachtet werden sollen:
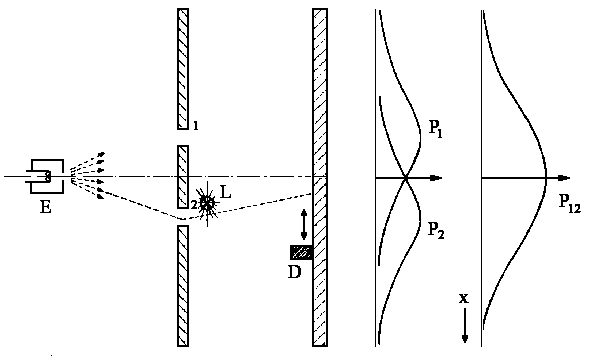 |
| Abb. 5: Streuversuch mit Elektronen, deren Durchgang durch die Löcher beobachtet wird. |
Das Ergebnis ist ernüchternd: Die beobachtete Elektronenverteilung
auf dem Schirm entspricht genau der Verteilung bei dem abwechselnd zugehaltenen
Löchern. Es gilt wieder
| P12 = P1+P2 oder P12 = |φ1|2+|φ2|2 |
Fazit: Wenn wir ein Experiment durchführen, bei dem wir feststellen können, welchenWeg das Elektron geht, dann können wir zwar mit Bestimmtheit sagen, es hat diesen oder jenen Weg genommen, doch ist das Interferenzbild verschwunden. Wenn wir jedoch keine Möglichkeit haben das Elektron zu beobachten, d.h. grundsätzlich nicht wissen können welchen Weg das Teilchen nimmt, dann ist die Behauptung das Elektron geht entweder den Weg 1 oder den Weg 2 unsinnig. Wir dürfen nicht einmal behaupten, dass es durch das eine oder durch das andere Loch hindurchgegangen ist.
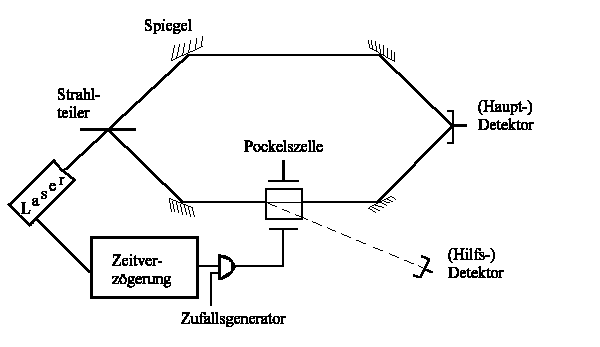
Was geschieht, wenn der Experimentator mit seiner Entscheidung, wie er das Teilchen beobachtet, wartet, bis das Teilchen den Doppelspalt durchdrungen hat und obendrein die beiden Wege weit voneinander entfernt liegen?
Im klärenden Experiment wird ein Laserstrahl auf einen Strahlteiler gelenkt und die so erzeugte Teilstrahlen werden nach der Wiedervereinigung auf einen Detektor gerichtet. Da es unmöglich ist zu sagen, ob ein einzelnes Photon den einen oder den anderen Weg vom Strahlteiler aus genommen hat, erhält man am Detektor eine Interferenz. Nun wird eine Pockelszelle in einen Teilstrahl eingefügt. Bei Anlegen einer Spannung wird ein Photon auf einen Hilfsdetektor gelenkt. Ohne Spannung bleibt alles beim alten. Ein Zufallsgenerator schaltet die Zelle ein oder aus nachdem das Photon den Strahlteiler bereits passiert hat, aber natürlich vor Erreichen des Detektors. Es zeigt sich wiederum, dass bei eingeschalteter Pockelszelle das Photon entweder den einen oder den anderen Weg genommen hat. Bei ausgeschalteter Zelle erscheint ein Interferenzmuster - das Photon hat beide Wege durchlaufen.
Dieses "Doppelspaltexperiment" zeigt auch, dass die beiden Wege beliebig weit voneinander entfernt leigen können. Im Prinzip können die beiden Teilstrahlen jeweils 1 Lichtjahr in entgegengesetzte Richtungen laufen, bevor sie wieder zur Interferenz zusammengefügt werden. Sowie die Pockelszelle so geschaltet wid, dass man weiß welchen Weg das Licht genommen hat, "weiß" das Photon über Lichtjahre hinweg instantan, wie es sich zu verhalten hat.
Versuche mit Atomen
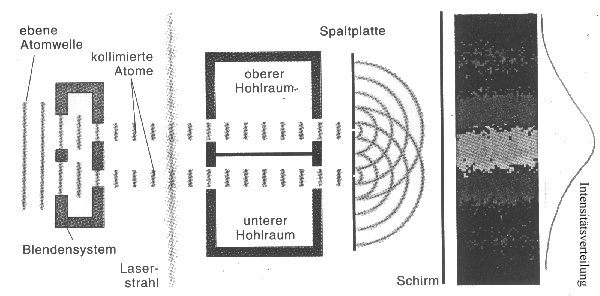 |
| Abb. 6: Bei einem Doppelspalt-Experiment mit Welcher-Weg-Detektoren werden Atome nach Passieren eines Blendensystems durch einen Laserstrahl angeregt. Die Atome fallen dann auf einen niedrigeren Energiezustand zurück, indem sie in dem Hohlraum, den sie jeweils durchqueren, ein Photon hinterlassen. Weil bei diesem Vorgang die Bewegung des Atoms nicht beeinflußt wird, kommt die Unbestimmbarkeitsrelation hier nicht ins Spiel. Trotzdem zeigt die Analyse des Versuchs, dass die Informationen "welcher Weg wurde genommen" die Entstehung von Interferenzmustern ausschliesst. |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.