Es ist grundsätzlich unmöglich, fundamentale Prinzipien in Form von Grundgleichungen, wie die bald folgende Schrödinger-Gleichung, zwingend abzuleiten. Man kann (und muss) versuchen, durch heuristische Gedankengänge den Sachverhalt (spielerisch) zu erfassen und dann die Lösungsvielfalt der „erdachten“ Gleichung mit den experimentellen Fakten (die nachprüfbar, sprich wiederholbar sein müssen) zu vergleichen. Eine solche Herleitung der Schrödingergleichung gibt's hier.
Danach ist die Wahrscheinlichkeitsamplitude ψ über eine partielle Differentialgleichung gegeben, die für zeitunabhängige Vorgänge in einer Dimension x die folgende Form annimmt:
| zeitunabhängige Schrödinger-Gleichung |
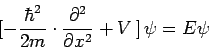 |
dabei ist V(x) das Potential in dem Sich das Teilchen bewegt. Wenn wir
den Ausdruck mit der partiellen Ableitung 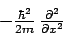 gleich
gleich 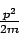 setzen, was genau
der kinetischen Energie entspricht, dann sehen wir, dass die Gleichung
die Energieerhaltung widerspiegelt. Wenn man noch E durch
setzen, was genau
der kinetischen Energie entspricht, dann sehen wir, dass die Gleichung
die Energieerhaltung widerspiegelt. Wenn man noch E durch 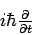 ersetzt,
dann erhält man die
ersetzt,
dann erhält man die
| zeitabhängige Schrödinger-Gleichung |
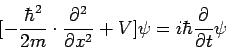 |
Eine Erweiterung auf drei Dimensionen (x,y,z) erhält man sofort,
indem man den 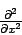 -Term durch
-Term durch 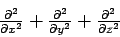 ersetzt. Erwin Schrödinger hat übrigens als erstes diese Gleichung
für das Wasserstoffatom (also als dreidimensionales Problem) gelöst,
was natürlich wie ein Paukenschlag die Wissenschaftlergemeinschaft
traf, denn alle beobachteten Phänomene konnten plötzlich quantitativ
exakt erfasst werden. Alle experimentellen Überprüfungen zeigen,
dass in der nichtrelativistischen Quantenmechanik die Schrödinger-Gleichung
voll gültig ist. Da in der Chemie immer alle molekularen Prozesse
deutlich kleiner als mit der Lichtgeschwindigkeit ablaufen, ist die Schrödinger-Gleichung
für den Chemiker die Fackel der Wahrheit, die etwas Licht in das finstere
Reich der Begegnung zwischen Atomen oder Molekülen bringt.
ersetzt. Erwin Schrödinger hat übrigens als erstes diese Gleichung
für das Wasserstoffatom (also als dreidimensionales Problem) gelöst,
was natürlich wie ein Paukenschlag die Wissenschaftlergemeinschaft
traf, denn alle beobachteten Phänomene konnten plötzlich quantitativ
exakt erfasst werden. Alle experimentellen Überprüfungen zeigen,
dass in der nichtrelativistischen Quantenmechanik die Schrödinger-Gleichung
voll gültig ist. Da in der Chemie immer alle molekularen Prozesse
deutlich kleiner als mit der Lichtgeschwindigkeit ablaufen, ist die Schrödinger-Gleichung
für den Chemiker die Fackel der Wahrheit, die etwas Licht in das finstere
Reich der Begegnung zwischen Atomen oder Molekülen bringt.
 Die Wellenfunktion ψ hat, dies sei noch einmal zur Erinnerung erwähnt,
keine direkte
physikalische Bedeutung, wenn auch mit ihrer Hilfe der Ablauf von Vorgängen
im Mikrokosmos beschrieben werden kann. Da wir davon ausgehen können,
das Teilchen irgendwo im Raum zu finden, d.h. die Wahrscheinlichkeit dafür
1 ist, muss die Normierungsbedingung gelten:
Die Wellenfunktion ψ hat, dies sei noch einmal zur Erinnerung erwähnt,
keine direkte
physikalische Bedeutung, wenn auch mit ihrer Hilfe der Ablauf von Vorgängen
im Mikrokosmos beschrieben werden kann. Da wir davon ausgehen können,
das Teilchen irgendwo im Raum zu finden, d.h. die Wahrscheinlichkeit dafür
1 ist, muss die Normierungsbedingung gelten:
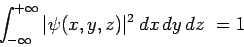 |
Der Ausdruck |ψ(x,y,z)|2dxdydz gibt die Wahrscheinlichkeit P(x,y,z) an, das Teilchen am Ort (x,y,z) im Volumenelement dV = dxdydz zu finden. P(x,y,z) hat im Gegensatz zu ψ(x,y,z) eine direkte physikalische Bedeutung, da die Wahrscheinlichkeit gemessen werden kann.
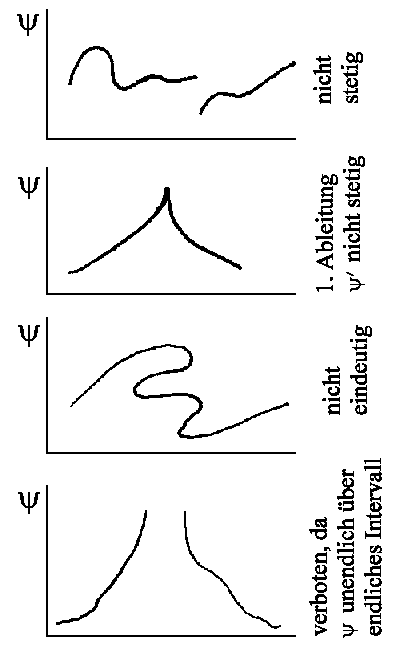
Weitere Anforderungen an ψ:
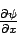 , d.h. die erste Ableitung muss ebenfalls stetig sein, solange sich
das Potential "vernünftig" verhält. (z.B. geht auch das
1/r-Potential
bei r = 0)
, d.h. die erste Ableitung muss ebenfalls stetig sein, solange sich
das Potential "vernünftig" verhält. (z.B. geht auch das
1/r-Potential
bei r = 0)![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.