Die Schrödingergleichung - Eine "Herleitung"

Gleich am Anfang sei gesagt, dass es grundsätzlich nicht möglich ist, die fundamentalen Prinzipien in Form von Grundgleichungen, wie es die bald folgende Schrödinger-Gleichung ist, zwingend abzuleiten. Man kann (und muss) versuchen, durch heuristische Gedankengänge den Sachverhalt (spielerisch) zu erfassen und dann die Lösungsvielfalt der „erdachten“ Gleichung mit den experimentellen Fakten (die nachprüfbar, sprich wiederholbar sein müssen) zu vergleichen. Also los:

Wir haben bereits gesehen, dass es möglich ist, Beobachtungen durch Betragsbildung von Wahrscheinlichkeitsamplituden zu beschreiben. Es gilt für eindimensionelle Wellen

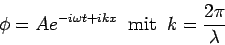
nach de Broglie gilt für jedes Teilchen mit dem Impuls p: λ = ^h/_p und für die Energie können wir schreiben E = hν = hω. Dies setzen wir in die obige Gleichung für φ ein; da wir die Gleichung durch die Beziehungen für λ und ω strapaziert haben, ersetzen wir noch φ durch den Buchstaben ψ für die Wahrscheinlichkeitsamplitude

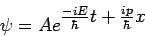
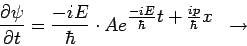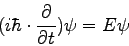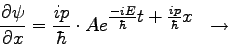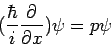Auf der rechten Seite der beiden Gleichungen stehen die Größen E und p, die ich im Experiment messen kann; es handelt sich um reale Zahlen (die mit ψ multipliziert werden). Auf der linken Seite der Gleichung steht eine Vorschrift, wie ich zu E bzw. p komme: Ich muss ψ nach t differenzierten (und mit ih multiplizieren), dann erhalte ich Eψ; differenziere ich nach x (und multipliziere mit ^h/_i), dann erhalte ich pψ. Man bezeichnet solche Rechenvorschriften in der Quantenmechanik allgemein als Operatoren. Wir haben sie zwar bereits am Ende des letzten Kapitels eingeführt, doch nun können wir die Zuordnung treffen:
 

Energie	E	→		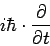Energieoperator ≡ H
Impuls	p	→		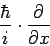Impulsoperator ≡ p
Ort	x	→	x
zur Kennzeichnung von Operatoren verwenden wir fette Symbole

klassisch	Operator

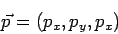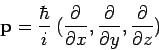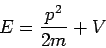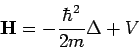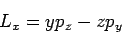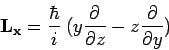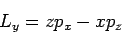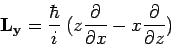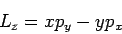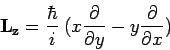Δ ist Symbol für den Laplaceoperator, dieser ist definiert als .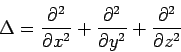

Wir wissen, dass die Energieerhaltung E = E_kin + E_pot gelten muss. Schreiben wir für die potentielle Energie direkt das Potential V(x) hin und für 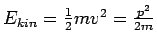und multiplizieren die Gleichung mit ψ:

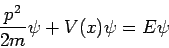
und ersetzen den Impuls durch seinen Operator

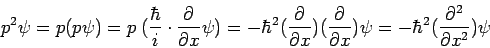
sowie die Energie E durch den Operator 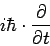,dann erhalten wir die

zeitabhängige Schrödinger-Gleichung (eindimensionaler Fall)

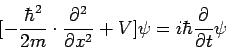Schnell noch die Erweiterung der Schrödinger-Gleichung auf die drei Raumdimensionen x, y, z:

		→
		→

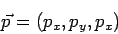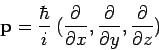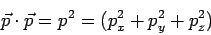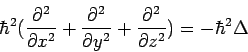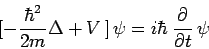Bei Verwendung des Hamiltonoperators für den Summenterm innerhalb der eckigen Klammern erhalten wir die

zeitabhängige Schrödinger-Gleichung (dreidimensionaler Fall, Kurzschreibweise)

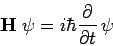Hängt das Potential (oder allgemein H) nicht von der Zeit ab und liegen scharfe Energiewerte E vor, dann kann man die Zeitabhängigkeit in der obigen Differentialgleichung durch folgenden Ansatz loswerden:

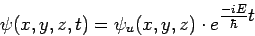Einsetzen in DGL:

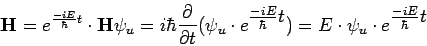
Dies führt uns auf die Kurzschreibweise der

zeitunabhängigen Schrödinger-Gleichung

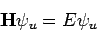Diese DGL gilt für scharfe Energiewerte E, die in der Quantenmechanik als stationäre Zustände bezeichnet werden. Kennen wir die zeitunabhängige Lösung ψ_u, dann können wir sofort die zeitabhängige hinschreiben, falls H nicht eine explizite Funktion von t ist und ψ_u stationäre Zustände mit scharfer Energie E beschreibt:
 

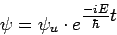Da wir davon ausgehen können, das Teilchen irgendwo im Raum zu finden, d.h. die Wahrscheinlichkeit dafür 1 ist, muss die Normierungsbedingung gelten

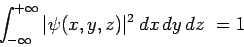Der Ausdruck |ψ(x,y,z)|²dxdydz gibt die Wahrscheinlichkeit P(x,y,z) an, das Teilchen am Ort (x,y,z), das heißt im Bereich [x,x+dx], [y,y+dy] und [z,z+dz] zu finden. P(x,y,z) hat im Gegensatz zu ψ(x,y,z) eine direkte physikalische Bedeutung, da Wahrscheinlichkeiten gemessen werden können. Die Wahrscheinlichkeitsamplitude ψ beschreibt das betrachtete System vollständig und erhält daher alle Informationen, die wir über das jeweilige System erhalten können.
 
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.