Unterscheidbare und identische Teilchen

Die Wahrscheinlichkeit P(φ) ein Teilchen unter dem Winkel φ zu finden, hängt davon ab, ob f(φ) die Amplitude der Streuung für

unterscheidbare Teilchen ist:

nicht unterscheidbare Teilchen ist:

P_u(φ) = |f(φ)|² + |f(π-φ)|²

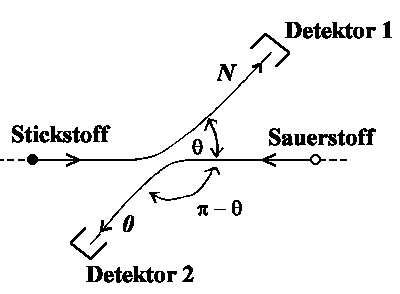
z.B. Stickstoff und Sauerstoffatome.

Der Detektor soll hier für N- und O-Atome empfindlich sein, ohnesie zu unterscheiden. Obwohl wir so nicht zwischen N und O unterscheiden, könnten wir es aber prinzipiell! Daher werden die Wahrscheinlichkeiten und nicht die Amplituden addiert.

P_i(φ) = |f(φ) + f(π-φ)|²

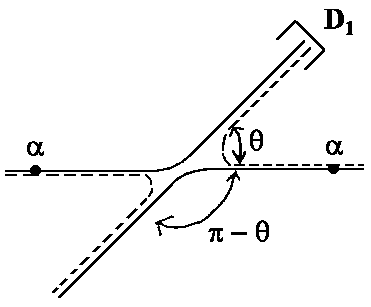
z.B. α-Teilchen (Heliumkerne, He⁺⁺)

Da es zwei Möglichkeiten gibt, ein α-Teilchen in den Zähler zu bekommen, nämlich Streuung des α-Teilchens in einem Winkel φ oder im Winkel π-φ können wir prinzipiell nicht unterscheiden, ob das bombardierende Teilchen oder das Targetteilchen in den Detektor gelangt.

Für den Streuwinkel φ = ^π/₂ gilt offenbar f(φ) = f(π-φ), das heißt:

P_u(^π/₂) = |f(^π/₂)|²+|f(^π/₂)|²
= 2|f(^π/₂)|²

P_i(^π/₂) =|f(^π/₂) + f(^π/₂)|²
= 4|f(^π/₂)|²

Die Natur macht es uns leider noch etwas schwieriger, wenn wir uns die Streuung von identischen Elektronen ansehen. Für diesen Fall findet man:

P_i(Elektronen) = |f(φ)−f(π-φ)|²

Also gilt

für φ = ^π/₂: P_i (^π/₂)= 0

Beim Elektron stellt man fest, dass sich mal zwei Elektronen wie identische Teilchen, andere Elektronen aber auch wie unterschiedliche Teilchen verhalten können, d.h. die Elektronen müssen noch ein weiteres Merkmal haben, das sie unterschiedlich machen kann. Diese interne Elektroneneigenschaft ist der Spin! (Stern-Gerlach Versuch). Man stellt fest, dass es nur zwei Arten von Elektronen gibt, d.h. der Spin tritt in zwei Ausprägungen auf, die wir mit Spin up und Spin down kennzeichnen wollen. Zwei miteinander stoßende Elektronen mit jeweils Spin up, ebenso zwei miteinander stoßende Elektronen mit jeweils Spin down, verhalten sich im Streuexperiment immer wie identische Teilchen, d.h. es gibt keine weitere Struktur, die sie unterscheidet und es gilt daher:

P_i = |f(φ) −f(π-φ)|²

Stößt hingegen ein Elektron mit Spin up auf ein Elektron mit Spin down, dann sind es zwei unterscheidbare Teilchen und es gilt

P_u = |f(φ)|²+|f(π-φ)|²

Beim Elektron ist der Spin s = ½ (mit den beiden Einstellmöglichkeiten m_s= +½ und m_s= -½ für Spin up und Spin down). Der Wert des Spins kann für andere Teilchen aber auch von ½ abweichen und teilt so die Teilchen in zwei Klassen:

Boseteilchen (Spin ganzzahlig, z.B. α-Teilchen, Photonen)

f(φ) + f(π-φ)

Fermiteilchen (Spin halbzahlig, z.B. Elektronen, Myonen)

f(φ) − f(&pi - φ)

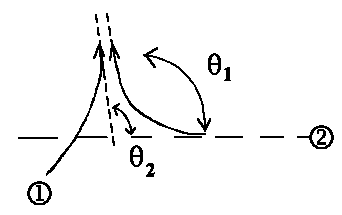Stellen wir uns nun zwei identische, also nicht unterscheidbare, Fermiteilchen vor, die in zwei nahe beieinander liegenden Richtungen gestreut werden, dann sind die Streuamplituden f(φ₁) und f(φ₂). Für die Wahrscheinlichkeit von Fermiteilchen gilt, dass die Streuamplituden subtrahiert werden müssen:

P_i = |f(φ₁) −f(φ₂)|²

Falls sich die beiden Teilchen auf gleichen Bahnen bewegen sollen, ist φ₁ = φ₂ und daher

P_i = 0 !!!

D.h. zwei Elektronen mit gleichem Spin können sich niemals am gleichen Ort befinden. Dies ist das berühmte Pauli'sche Ausschließungsprinzip (Wolfgang Pauli).

Der Spin wird uns noch reichlich bei den Atom- und Molekülspektren begegnen. Doch kehren wir noch einmal zu unserem Doppelspaltexperiment zurück, damit wir das überraschende Verhalten von Teilchen besser mathematisch beschreiben können. Dabei werden uns seltsame Klammern und Wellenfunktionen begegnen.

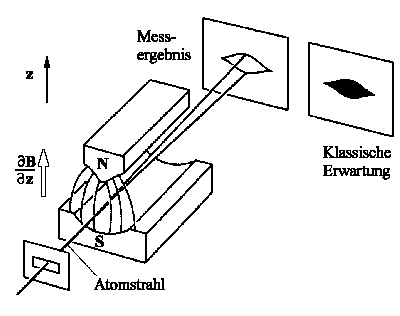Der Stern-Gerlach-Versuch schematisch: Der Atomstrahl durchfliegt ein homogenes Magnetfeld. Man beobachtet eine Aufspaltung des Strahls in nur zwei Komponenten, die als Spin up und Spin down bezeichnet werden. Klassisch wären alle Bereiche zu erwarten.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.