 |
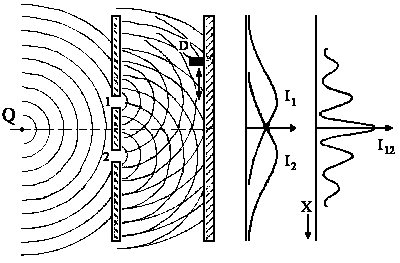
| Beugungsversuch mit Wellen |
|
|
Allgemein gilt für eine Welle:
| f = Ae−iwt+ikx
w=2pn: Frequenz der Welle k = 2π/l = p/ |
Die Intensität I der Welle ist durch das Betragsquadrat gegeben: I = |f|2. Das Betragsquadrat einer komplexen Zahl c berechnen wir allgemein durch |c|2 = c·c* ; c* kennzeichnet die konjugierte Zahl zu c, also das Ersetzen von i durch -i ( i ® -i ).
Für die Intensität einer Welle gilt also: I = |f|2 = |Ae−i(wt−kx). A*e+i(wt−kx)| = |A|2
In der Abbildung entstehen zwei Wellen an den Löchern 1 und 2 und überlagern sich beim Detektor D zu einer Gesamtintensität I. Die Intensität zweier sich überlagernder Wellen f1 und f2 der gleichen Frequenz, aber unterschiedlicher Phase ist dann:
f1 = A1e−iwt+ikx und f2 = A2e−iwt+ikx+ij mit j = Phasenverschiebung
I = |f1+f2|2 = (f1+f2) · (f1*+f2*) = |f1|2 + |f2|2 + f1*·f2 + f1·f2*
I = I1 + I2 + A1*A2eij + A1A2*e−ij
Weiterhin gilt: A1A2 = (I1I2)½
und
eix = cos x + isin x bzw.
e-ix = cos x - isin x, d.h. eij
+ e−ij
= 2 cos j, denn
eij + e−ij
= cos j + isin j
+ cos (-j) + isin (-j)
= 2 cos j
|
|
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.