Dieses Kapitel beginnt mit einer allgemeinen mathematischen Abhandlung.
Wer lieber zu einem einfachen Beispiel möchte, das alles relevante
enthält, klickt hier.
Messen wir den n-Energiezustand (z.B. unseres Teilchens im Kasten),
dann entspricht dies mathematisch
| H |n> = | En | |n> | Hyn = | En yn | |
| Energieoperator ¾ . | ¾¾¾¾ Eigenfunktion | ¾¾ | |||
| ¾¾¾¾ Eigenwert ¾¾¾¾ | |||||
Anwenden von <m| (Eigenfunktion) bzw.
Integration ò ym*.....dV
auf die jeweilige Gleichung ergibt
| <m|H|n> = En <m|n> | ò ym* Hyn dV = En ò ym* yn dV | |
| = En δm,n . | = En δm,n . |
Wir können die Größe <m|H|n>
bzw. ò ym*
yn
dV duch Hmn abkürzen und als Matrix auffassen, die im Falle
von Eigenfunktion nur Diagonalelemente enthält, die ungleich0 sind:
| <m|H|n> = Hmn ≡ | æ
ç ç ç ç ç ç è |
H11 | H12=0 | ... | H1n=0 | ü
ú ú ú ú ú ú ø |
= | æ
ç ç ç ç ç ç è |
E1 | 0 | ... | 0 | ü
ú ú ú ú ú ú ø |
| H21=0 | H22 | ... | H2n=0 | 0 | E2 | ... | 0 | ||||||
| ...
... ... |
...
... ... |
...
... ... |
...
... ... |
...
... ... |
...
... ... |
...
... ... |
...
... ... |
||||||
| Hn1=0 | Hn2=0 | ... | Hnn | 0 | 0 | ... | En |
In diesem Fall geben die Diagonalelemente der Matrix also die Energieeigenwerte des Systems wieder. Voraussetzung ist aber, dass |n> bzw. |m> Eigenfunktionen sind. Wie sieht das Gleichungssystem aus, wenn nur "Nichteigenfunktionen" bekannt sind? Zur Analyse des Systems entwickeln wir die Eigenfunktion |n> nach einem anderen Basissatz, wobei die entsprechenden Basisvektoren |i> dann natürlich nicht mehr Eigenfunktion bzgl. H|i> sind.
|n> = Σi ai|i> yn = Σi ai φi
Einsetzen in unsere Schrödingergleichung (mit En = E):
H|n> = E|n> H yn = E yn
H Σi ai|i> = E Σi ai|i> H Σi ai φi = E Σi ai φi
Anwenden von <k| bzw òfk*...dV (<k| ist orthogonal zu |i>)
Σi ai <k|H|i> = E Σi ai <k|i> Σi ai òfk* Hφi dV = E Σi aiòfk* φi dV
Σi ai Hki = E ak Σi ai Hki = E ak
Dies ist ein lineares Gleichungssystem:
| i → | a1 H11 | + | a2 H12 | + | a3 H13 | + | ... | = E a1 |
| ¯ k | a1 H21 | + | a2 H22 | + | a3 H23 | + | ... | = E a2 |
| a1 H31 | + | a2 H32 | + | a3 H33 | + | ... | = E a3 | |
| .
. . |
.
. . |
.
. . |
.
. . |
Solche linearen Gleichungssysteme sind in der Algebra seit langem bekannt:
| . | = E . |
||
| Matrix¾ | ¾Vektor¾ | ||
Es gibt entsprechende Verfahren, um die Eigenwerte E zu bestimmen und um eine Transformation durchzuführen, die uns die Eigenfunktion (hier Eigenvektoren) liefert.
Wir wollen es uns einfach machen und ein System mit nur zwei Zuständen
betrachten, das uns aber sehr viele Phänomene in der Spektroskopie
und Chemie erklären kann. Z.B. können wir uns Benzol durch folgende
elektronische Struktur zusammengesetzt denken:
| Benzol ≡ | 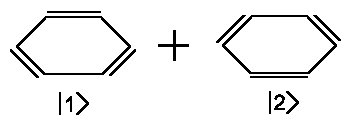 |
|Benzol> = a1|1>
+ a2|2>
H |Benzol> = E |Benzol> |
Multiplikation mit <1|:
a1 <1|H|1>
+ a2 <1|H|2>
= a1 E
bzw. <2|:
a1 <2|H|1>
+ a2 <2|H|2>
= a2 E
Mit dem entsprechenden Abkürzungen <1|H|1>
= H11 etc., erhalten wir das Ergebnis das mit dem für beliebig
viele Zustände (s.o.) übereinstimmt.
| H11 a1 + H12 a2 = E a1 | ® | a1/a2 = H12/E − H11 | }gleichsetzen |
| H21 a1 + H22 a2 = E a2 | ® | a1/a2 = E − H22/H21 |
® H12 · H21 = (E − H22) ( E − H11)
E2 − (H22 + H11) E = H12 · H21 − H11 · H22
→
| EI,II = H11 + H22/2 ± [(H11− H22)²/4 + H12 H21]½ |
Es gibt also zwei stationäre Energiezustände EI und EII. Falls H12 = H21 = 0 ist, also irgendwelche Wechselwirkungen zwischen den Zuständen |1> und |2> nicht stattfinden, dann ist EI = H11 ≡ E1 und EII = H22 ≡ E2. EI und EII entsprechen dann den Energiewerten der ungestörten Zustände:
H12 = H21 = 0 → EI,II = (H11 + H22)/2± (H11− H22)/2
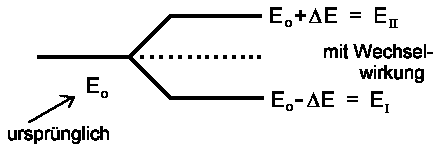
Die Gleichungen werden noch einfacher, wenn die Terme H11
und H22 gleich sind (wie beim Benzol): H11 = H22
= E0. Bezeichnen wir noch die Wechselwirkung H12
= H21 mit −ΔE, dann beträgt
die Energie der stationären Zustände |I>
und |II>:
| EII,I = E0 ±DE |
 |
Wir haben nun die Energie der stationären Zuständen |I>
und |II>. Doch wie sieht die Wellenfunktion
aus? Nun, im betrachteten Beispiel (H11 = H22 = E0
und H12 = H21 = −ΔE) können
wir die Wellenfunktion sehr einfach aus den (bekannten) Wellenfunktionen
für die Zustände |1> und |2>
konstruieren. Zunächst die Lösung:
| |I> = 1/Ö2(|1> + |2>) |II> = 1/Ö2(|1>- |2>) |
Nun der Beweis über Normierung, Orthogonalität und diagonale Energiematrix:
a) Normierung
= ½ (<1|1> + <2|1> + <1|2> + <2|2>) = ½ (<1|1>-<2|1>-<1|2> + <2|2>)
= ½ (1 + 0 + 0 + 1) = ½ (1 − 0 − 0 + 1)
<I|I> = 1 <II|II> = 1
b) Orthogonal
<I|II> = 1/Ö2(<1| + <2)1/Ö2(|1> - |2>)
= ½ (<1|1> + <2|1> -<1|2>-<2|2>)
= ½ (1 + 0 − 0 − 0 − 1)
® <I|II> = <II|I> = 0 (als Übung beweisen)
c) Die Energiematrix ![]() muss für Eigenvektoren |I>, |II> diagonal sein:
muss für Eigenvektoren |I>, |II> diagonal sein:
HI,I = <I|H|I> = ½ (<1| + <2|) H (|1> + |2>)
= ½ (H11 + H21 + H12 + H22) = ½ (E0 −ΔE −ΔE + E0) = E0−ΔE = EI
HI,II = <I|H|II> = ½ (<1| + <2|) H(|1>- |2>)
= ½ (H11 + H21 − H12 − H22) = ½ (E0 − ΔE + ΔE − E0) = 0
HII,I = <II|H|I> = ½ (<1| -<2|)H(|1> + |2>)
= ½ (H11 − H21 + H12 − H22) = ½ (E0 + ΔE −ΔE − E0) = 0
HII,II = <II|H|II> = ½ (<1| -<2|)H(|1>- |2>)
= ½ (H11 − H21− H12 + H22) = ½ (E0 + ΔE + ΔE + E0) = E0 + ΔE = EII
Im allgemeinen Fall H11 ¹ H22, H12 ¹ H21 sind die stationären Zustände |I>, |II> mit den ursprünglichen Zuständen |1> und |2> über
|I> = |1> a1I + |2> a2I (für EI) |II> = |1> a1II + |2> a2II (für EII)
verbunden. Die i. a. komplexen Konstanten erfüllen die Gleichungen:
a1I/a2I = H12/(EI - H11) |a1I|2 + |a2I|2 = 1
a1II/a2II = H12/(EII - H11) |a1II|2 + |a2II|2 = 1
Einige einfache chemische Anwendungen für Ammoniak, H2+ und H2 gibt's hier.
Bindung von verschiedenen Ionen durch ein Elektron
Zweiatomige unsymmetrische Molekülionen besitzen oft eine schwache Bindung. Warum ?
Betrachten wir z.B. ein Proton und ein positives Li-Ion, also zwei Teilchen mit einer positiven Ladung. Jetzt sind die ursprünglichen Terme H11 und H22 völlig unterschiedlich und die Differenz |H11− H22| >>DE. Wir erhalten dann (für H12 = H21 = −ΔE):
EI,II = (H11+H22)/2 ± (H11−H22)/2[1 + 4ΔE²/(H11−H22)²]½
Da x = 4ΔE2/(H11−
H22)2 klein gegen 1 ist und in erster Näherung
(1 + x)½ ≈
1 + x/2 gilt, erhalten wir:
| EII = H22 + ΔE²/(H22−H11) | 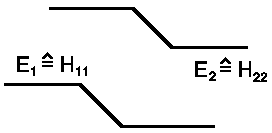 |
| EI = H11 -DE²/(H22−H11) |
Die zusätzliche Energieaufspaltung durch den "Austauschsterm" ΔE²/(H22−H11) ist in diesem Fall kleiner als beim H2+.
(EII−EI)/(EII−EI)H2+ = 2ΔE²/(H22−H11)/2ΔE = ΔE/(H22−H11) << 1
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.