Summiere und erkläre (1) - Benzol

Dank des Doppelspaltexperiments kennen wir bereits ein wesentliches Prinzip der Quantenmechanik, nämlich dass sich die richtige Wahrscheinlichkeitsamplitude zur Beschreibung eines Systems als Linearkombination der Einzelamplituden darstellen läßt. Wir wollen es uns einfach machen und ein System mit nur zwei Zuständen betrachten, das uns aber sehr viele Phänomene in der Spektroskopie und Chemie erklären kann (eine allgemeine Behandlung gibt's hier). Wir können uns z.B. Benzol durch folgende elektronische Struktur zusammengesetzt denken:
 

Benzol  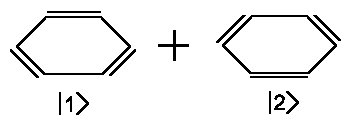≡ &psiBenzol = a1&phi1+ a2φ2
Die linke Elektronenkonfiguration soll durch φ1 (bzw. durch |1>) und die rechte durch φ2 (bzw. durch |2>) beschrieben werden. Das "richtige" Benzol wird nun durch die Linearkombination ψBenzol= a1φ1+ a2φ2 (bzw. |Benzol> = a1|1> + a2|2>) korrekt beschrieben, wobei die Koeffizienten a1 und a2 die relativen Anteile angeben. Wir wollen nun die Frage beantworten, wie groß diese Anteile sind und welche Energie E das Benzol haben kann. Sicherlich wird uns an diesem Punkt etwas mulmig, denn wir wissen weder, wie die Einzelamplituden |1> und |2> aussehen, noch welche Energie Benzol in der Konfiguration |1> bzw. |2> besitzt. Wir tun einfach so, als ob wir das wüßten! Etwas wissen wir schon: Die Konfigurationen sind äquivalent und die entsprechenden Energien müssen also gleich sein. Wir kennzeichnen sie daher beide durch die Energie Eo. Die ganz Schnellen unter uns werden sagen, dass dann auch die Koeffizienten exakt gleich sein müssen. Doch halt: nur die Betragsquadrate geben uns die Wahrscheinlichkeit an, Benzol in der Konfiguration |1> bzw. |2> zu finden und daher können wir höchstens fordern:
|a1|2=|a2|2.  Doch mit ganz wenig Mathe kriegen wir alles raus:
Die Schrödingergleichung für das Benzol lautet einfach:

 HψBenzol  =  E ψBenzol

 
wobei wir natürlich weder ψBenzol noch den Hamiltonoperator H kennen. Immerhin können wir für ψBenzol unsere Linearkombination einsetzen:
 H (a1|1>+a2|2>)  =  E (a1|1>+a2|2>)

Nun der "Trick": Ausklammern und

 Multiplikation mit <1|:         a1 <1|H|1> + a2 <1|H|2>  =  E <1|a1|1> + E<1|a2|2> =  a1 E
                   bzw. <2|:         a1 <2|H|1> + a2 <2|H|2>  =  E <2|a1|1> + E<2|a2|2> =  a2 E

Das letzte Gleichheitszeichen ergibt sich, da <1|1> = 1 und <1|2> = 0 ist, denn die Zustände sollen orthonormal sein. Die Größen <1|H|1> und  <2|H|2> sind die Energien von Benzol nur in der Konfiguration |1> bzw. |2>, die wir wie gesagt mit Eo abkürzen wollen. <1|H|2> und <2|H|1> ist ein Maß dafür, wie groß die Chance ist, dass das System von der Konfiguration |2> in die Konfiguration |1> bzw. von der Konfiguration |1> in die Konfiguration |2> = übergeht.  Offensichtlich geht es von der einen zur anderen Konfiguration genauso gut (oder schlecht) wie von der anderen zur einen, d.h. es gilt sicherlich: <1|H|2>= <2|H|1>, wofür wir die Abkürzung W wählen. Wir erhalten dann die zwei Gleichungen (die wir nach a1/a2 auflösen):

Eo a1 + W a2  =  E a1 → a1/a2  =  W/E − Eo }gleichsetzen
W a1 + Eo a2  =  E a2 → a1/a2  =  E − Eo/W
→  W · W  =  (E − Eo) ( E − Eo)
→  (E− Eo)2 =  W2
→   EI,II  =  Eo ± W

Es gibt also zwei stationäre Energiezustände EI und EII, von denen der eine Zustand energetisch tiefer liegt als der Ausgangszustand Eo und der andere liegt um den gleichen Betrag W höher als Eo. Gewöhnlich bezeichnet man den energetisch tieferen Zustand mit EI und den energetisch höheren mit EII, so dass wir eigentlich das ± umdrehen müßten; aber so pingelig wollen wir nicht sein. Falls W = 0 ist, also irgendwelche Wechselwirkungen zwischen den Zuständen |1> und |2> nicht stattfinden, dann entsprechen EI  und EII dem Energiewert Eo der ungestörten Zustände. Die Wechselwirkung W bezeichnen wir mit ΔE. Die Energie der stationären Zustände |I> und |II> beträgt dann

EI,II  =  Eo  ±ΔE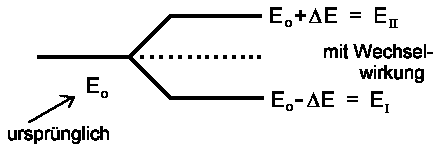

Wir haben nun die Energie für die stationären Zustände |I> und |II>. Doch wie sehen diese Zustände aus? Nun, wir brauchen nur in der obigen Formel a1/a2  =  E − Eo/W für E unsere neuen Energien EI,II  =  Eo±W einsetzen und erhalten sofort:
a1= ±a2, was wir uns schon eingangs überlegt hatten. Führt man noch die Normierung durch, d.h. <I|I>=1, bzw. <II|II>=1, dann kommt man schnell zur Lösung:

|I>  = 1/√2(|1> + |2>)               |II>  = 1/√2(|1>−|2>)

Alle diese Überlegungen gelten nicht nur für Benzol, sondern auch z.B. für das Ammoniakmolekül. Energiediagramme zeigt und eine praktische Anwendung behandelte der Abschnitt Ammoniak. Bei diesem Molekül machen sich nämlich Übergänge zwischen zwei möglichen Zuständen bemerkbar:
 

|NH3> |1> |2>
N-Atom oberhalb  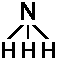unterhalb der Wasserstoffatome

Beim Benzol ist die Wechselwirkungsenergie groß, denn das leichte Elektron kann schnell zwischen den beiden Konfigurationen hin-und herwechseln. Das "Durchschwingen" beim Ammoniakmolekül erfolgt aufgrund der um mehrere Größenordnungen höheren Masse erheblich langsamer, d.h. die Wechselwirkungsenergie ist erheblich kleiner. Tatsächlich liegt der elektronische Übergang beim Benzol im UV und beim NH3 im fernen IR. In der folgenden Einheit werden wir denselben Ansatz zur Beschreibung des Wasserstoffmoleküls und des H2+ benutzen.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.