Vom Butadien zum Polyen

Vom Butadien zum Polyene
Der Teilchen im Kasten - Ansatz wird augenscheinlich

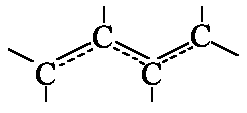Beim Butadien sind die π-Elektroden delokalisiert; sie können sich längs der C-C-Bindung (Länge etwa 139 pm) frei bewegen.
In konjugierten Systemen etc. haben die π-Elektronen die ganze Länge der Kette als Aufenthaltsort zur Verfügung. Sie verhalten sich wie ein "Elektronengas" in einer Dimension.

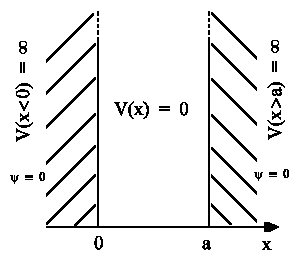Wir wollen zunächst untersuchen, wie sich ein Elektron verhält. Dazu idealisieren wir unser Polyen noch etwas weiter. Wir nehmen an, dass sich das Elektron von Ort 0 bis a völlig frei längs der x-Achse bewegen kann, d.h. V(x) = 0 für 0 < x <a. In den anderen Raumbereichen ist das Potential aber unendlich hoch; V(x ≤ 0; x ≥ a) → ∞. Da die potentielle Energie am Rand unendlich groß ist, kann das Teilchen sich nicht in der Wand aufhalten, d.h. wir fordern, dass die Randbedingungen

y(0) = 0 und y(a) = 0 erfüllt werden.

Dieses einfache Modell für die Beschreibung von Polyenen entspricht genau der Bewegung eines Teilchens im Potentialkasten, bei dem das Potential V(x) Innerhalb des Bereichs 0 < x < a Null ist. Im verhergegangenen Abschnitt erhielten wir als normalisierte Lösung der Schrödingergleichung die Wellenfunktionen zum n-ten Energiezustand:

ψ_n(x) = √(²/_a)·sin (nπx/a)

wobei den Zuständen folgende diskrete Energien zukommen

E_n = ^h²/_8ma² n² mit n = 1, 2, 3, ...

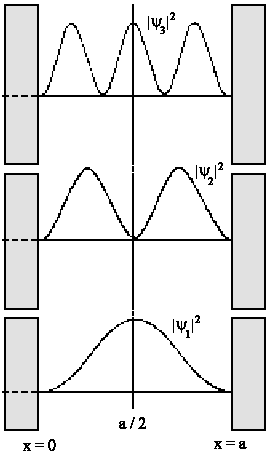
Anhand der Abbildung wird deutlich, dass nur die Wellenfunktionen möglich sind, die wie bei einer stehenden Welle in die Potentialwände passen. Der niedrigste Zustand n=1 ist derjenige mit nur einem Bauch und lediglich Nullstellen an der Wand. Bei jeder energetisch höheren Lösung kommt immer ein Knoten (ein Nulldurchgang) hinzu.

Bei den Polyenen werden nun alle vorhandenen Quantenzustände ihrer Energie nach mit Elektronen besetzt. Da Elektronen Fermionen sind und damit dem Paulischen Ausschließungsprinzip gehorchen müssen, erhalten wir unter Berücksichtigung des Spins für

Butadien

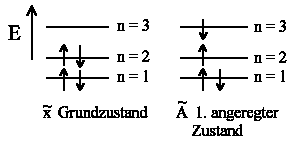Man kann bei Polyenen Absorptionsspektren beobachten und die Anregungsenergie ΔE entspricht dem Energieunterschied zwischen den beiden relevanten Niveaus (n+1) und n. Das im Grundzustand energetisch höchste Niveau, das mit Elektronen besetzt ist, bezeichnen wir als HOMO (highest occupied molecular orbital). Im Falle des Butadien ist dies n = 2. Das energetisch darüber liegende Niveau (also n+1=3 im Falle des Butadiens) wird als LUMO (lowest unoccupied molecualr orbital) bezeichnet. Da für eine Doppelbindung zwei Elektronen benötigt werden und nach dem Pauliprinzip sich die Elektronen voneinander unterscheiden müssen, können wir maximal zwei Elektronen (Spin up und Spin down) pro Quantenzustand n "unterbringen". D.h. die Gesamtzahl der Doppelbindungen entspricht gerade n und wir erhalten für den Energieunterschied ΔE = E_n+1− E_n:

ΔE = ^h²/_8ma²[(n + 1)² − n²] = ^h²/_8ma² (2n + 1) = hν = h^c/_λ

wobei λ der Absorptionswellenlänge entspricht. Wenn wir die Wellenlänge der Absorption messen, dann können wir daraus auch die Kettenlänge a experimentell bestimmen:

a_exp² = (2n+1) λ_exp^.
h/_8mc

Die Länge einer C-C-Bindung beträgt ca. a₀≈ 0,139 nm, so dass wir für die Länge der konjugierten Kette a_kk = a_o^.(2n−1) ansetzen können. Das Experiment liefert:

n	Stoff	λ_exp / nm	→a_exp / nm	a_kk / nm
2	Butadien	210	0,56	0,42
3	Hexatrien	247	0,72	0,70
4	Oktatetraen	268	0,88	0,98
5	Vitamin A	306	1,01	1,26
11	Carotin	420	1,70	2,94

Obwohl das Modell extrem einfach ist wurde, gibt es die Tendenz richtig wieder.

Und nun zu den elektrisch leitfähigen Polymeren:
Im Jahr 2000 wurde der Nobelpreis für Chemie für leitfähige Polymere an A.G. MacDiarmid, A.J. Heeger und H. Shirakawa vergeben. Die Leitfähigkeit von Metallen beruht darauf, dass den äußeren Elektronen energetisch höhere unbesetzte Zustände zur Verfügung stehen, in die sie thermisch - also mittels allgegenwärtiger Wärmeenergie - angeregt werden können: Bei Metallen grenzen besetzte und darüberliegende unbesetzte Zustände unmittelbar aneinander. Ganz anders bei Isolatoren: Hier klafft eine große Lücke zwischen dem höchsten besetzten Orbital (HOMO) und dem niedrigsten unbesetzten (LUMO). Konjugierte Polymere nehmen eine Zwischenstellung ein. Wir wollen nun zeigen, dass der energetische Abstand zwischen HOMO und LUMO mit wachsender Kettenlänge gegen null geht:

Setzen wir nämlich in unsere Gleichung für den Energieabstand zwischen LUMO und HOMO, ΔE = ^h²/_8ma²(2n+1), die Länge der konjugierte Kette mit a = a_o·(2n−1) ein, dann ergibt sich:

ΔE = h²/8ma_o² · ⁽²ⁿ⁺¹⁾/_(2n-1)²

Für große n ist ΔE = ^h²/_6mao²· ¹/_n, d.h. ΔE wird mit zunehmender Kettenlänge immer kleiner und die Leitfähigkeit nimmt zu, da die äußeren Elektronen immer leichter in die unbesetzten höheren Zustände gelangen können.

Genauere quantenchemische Betrachtungen zeigen jedoch, dass die Lücke zwar kleiner wird, aber bestehen bleibt, weshalb undotiertes Polyacetylen mit einer Leitfähigkeit von 10⁻⁷ bis 10⁻⁵ Siemens pro Meter nur ein Halbleiter ist. Der Grund dafür ist, dass wie bei der konventionellen Strichdarstellung von Polyacetylen jede zweite Bindung Doppelbindungscharakter hat.

Eine Dotierungssubstanz wie Iod sorgt dafür, dass mitten in der Bandlücke ein neuer Zustand auftritt, der entweder Elektronen aus dem HOMO aufnehmen oder an das LUMO abgeben kann und so die Leitfähigkeit erhöht.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.