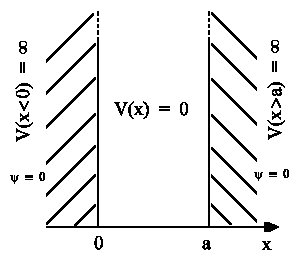Ein Teilchen im Kasten


Potentialkasten
Wir wollen die Schrödingergleichung für ein einfaches Problem lösen, das uns aber sehr viele wesentliche Merkmale der Vorgehensweise und der Interpretation der Lösung erläutert.
Wir nehmen an, dass sich ein Teilchen von Ort 0 bis a völlig frei längs der x-Achse bewegen kann, d.h. V(x) = 0 für 0 < x < a. In den anderen Raumbereichen ist das Potential aber unendlich hoch; V(x ≥0; x ≤ a) →∞. Da die potentielle Energie am Rand unendlich groß ist, kann das Teilchen sich nicht in der Wand aufhalten, d.h. wir fordern, dass die Randbedingungen

ψ(0)  =  0     und      ψ(a)  =  0
erfüllt werden.
Animation
Innerhalb des Bereichs 0 < x < a ist das Potential Null und wir müssen für diesen Bereich die Differentialgleichung −h²/2md²/dx²y - Eψ = 0 bzw.
  d²ψ/dx² + k²ψ  =  0     mit   k²  =  2mE/h² 
lösen

Mit dem Lösungsansatz ψ = Aeikx + Be-ikx (dies ist die Bewegung eines freien Teilchens von links nach rechts und umgekehrt) erfüllen wir die obige Schrödingergleichung (durch Einsetzen bestätigen); nur müssen noch die Randbedingungen erfüllt werden:

ψ(x=0)  =  A + B  =  0  →  B  =  −A
ψ(x)  =  A(eikx− e−ikx)  =  2iA sin kx  =  C sin kx

(C = 2 iA abgekürzte neue Konstante). Aus der zweiten Randbedingung ψ(x = a) = C · sin ka = 0  folgt entweder, dass sin ka = 0 ist oder dass C = 0 ist. C = 0 ist aber unsinnig, da wir dann niemals eine Wellenfunktion, sprich ein Teilchen, erhalten würden. Folglich muss gelten, dass der Sinus verschwindet, also  k · a = n . π

k  =  π/a· n          n = 1, 2, 3, ....

(n=0 entfällt, da auch dann ψ(x) für alle x gleich Null ist) oder nach Einsetzen für k und Auflösen nach E

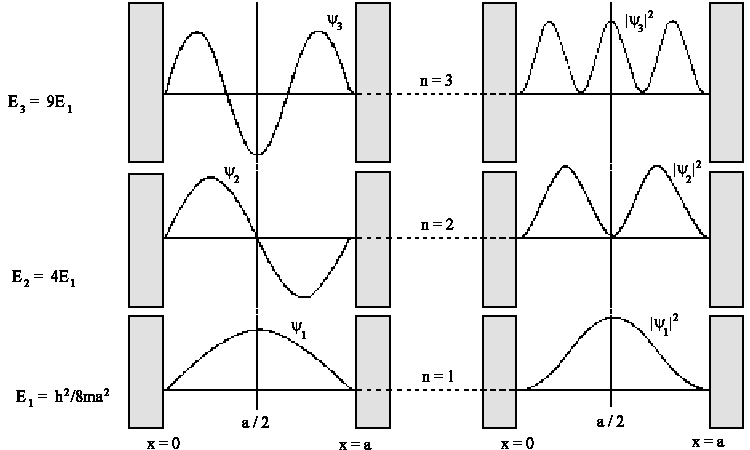
En  =  h²/8ma² n²

Für den Impuls p = (2mE)½ des Teilchens erhalten wir p = h/2a· n

Die Energie muss danach gequantelt sein, da n ganzzahlig ist. Die möglichen Energiezustände sind dann: E1 = h²/8ma² , E2 = 4E1 , E3 = 9E1 , E4 = 16E1 ,....   Die Energiequantelung erfolgt, da die Wellenfunktion durch das Potential und die Randbedingungen festgelegt ist.

Kasten_4.gif
Die kleinste Energie ist nicht Null, was uns aufgrund der Unschärferelation nicht überrascht. Da das Teilchen im Bereich 0 < x < a eingezwängt ist, muss es einen minimalen, aber endlichen Impuls und damit eine Energie größer Null besitzen. Die Wellenfunktionen zum n-ten Energiezustand lautet:
ψn(x)  =  C sin(nπx/a)

Die Größe C bestimmen wir über die Normalisierungsbedingung:

o∫a|ψn|2dx  =  1  =  o∫a C2 sin2(nπx/a)dx  =  C2 .  ½ a  =  1

ψn(x)  =  (2/a)½ sin(nπx/a)

Für die Beschreibung der Wellenfunktionen ψ und deren Betragsquadrate ist x = ½a besonders interessant. Für |ψ| liegt hier entweder ein Maximum (Bauch der stehenden Welle) oder der Funktionswert Null (Knoten der stehenden Welle) vor. Darüber hinaus stehen die Funktionswerte links und rechts dieses Punktes in einer einfachen Beziehung. Sie sind entweder identisch oder unterscheiden sich nur im Vorzeichen.

kugelsymmetrisches s-Orbital spiegelsymmetisches p-Orbital
ψA ψB
Allgemein sind Symmetrien der Wellenfunktionen ψ für Bindungen zwischen Atomen von größter Bedeutung. Bei Wechselwirkungen zwischen Materie und Licht wiederum stellt die gerade oder ungerade Parität einen wesentlichen Aspekt dar. Das Kriterium hierfür ist die Symmetrie bezüglich eines Punktes im Raum, es wird im Abschnitt Entartung ausführlich dargestellt.


Erweiterung auf drei Dimensionen

Die Erweiterung unseres Modells auf ein Teilchen innerhalb eines Potentialkastens mit den Begrenzungen 0<x<a, 0<y<b, 0<z<c, ist relativ einfach:

Schrödingergleichung:      −h²/2m(∂²/∂x² + ∂²/∂y² + ∂²/∂z²)ψ(x,y,z) - Eψ(x,y,z)  =  0
Separationsansatz:        ψ(x,y,z)  =  ψx(x) ·ψy(y) ·ψz(z)          k2  =  2mE/h²
Einsetzen:         ψyψz∂²/∂x²ψx + ψxψz∂²/∂y²ψy + ψxψy∂²/∂z²ψz + k2ψx(x)ψy(y)ψz(z)  =  0

Division durch   (ψx·ψy·ψz)   und setzen von   k2 = kx2 + ky2 + kz2  :
 

(1/ψx∂²/∂x²ψx + kx2)    +   (1/ψy∂²/∂y²ψy + ky2)    +  (1/ψz∂²/∂z²ψz + kz2)   =  0 
|¾¾¾¾¯¾¾¾¾|   |¾¾¾¾¯¾¾¾¾| |¾¾¾¾¯¾¾¾¾| 
  =  0    =  0    =  0 
→  gleiche DGLs wie im eindimensionalen Fall, denn einfache Umformung ergibt z.B. für x sofort:  ∂²/∂x²ψx + kx²ψx= 0 !

Wir erhalten daher für die Energiezustände, die möglich sind:

E  =  h²/8m(n1²/a² + n2²/b² + n3²/c²)

wobei n1, n2 und n3 die Quantenzustände für die x-, y- bzw. z-Richtung sind.

Die Wellenfunktion   ψ(x,y,z)  =  ψx(x) . ψy(y) ·ψz(z)   ist danach:

ψ(x,y,z)  =  C · sin(n1π x/a)· sin(n2πy/b)· sin(n3πz/c)

wobei C aus der Normierungsbedingung

o∫ao∫bo∫c |y(x,y,z)|2 dxdydz  =  1

zu berechnen ist.

Die Schreibweise nach Dirac für die ψ-Funktion lautet:

<x,y,z|n1n2n3>  =  C sin(n1πx/a)·sin(n2πy/b)·sin(n3πz/c)

Häufig schreibt man heute gekürzt und recht lax:  |n1n2n3> = C sin(n1πx/a) sin(n2πy/b) sin(n3πz/c), wobei implizit von den Ortskoordinaten x, y, z ausgegangen wird (jedoch müßte man korrekt <x|n> schreiben, da erst so die Ortsdarstellung zu entnehmen ist).
Die Normierungsbedingung ist in jedem Fall:

<n1n2n3|n1n2n3>  =  1

Wir erhalten also für die Normierungskonstante C  = (2/a)1/2 (2/b)1/2 (2/c)1/2 = (8/abc)1/2.
Falls die Begrenzungen des Kastens alle gleich lang sind, d.h. a = b = c, dann entsteht eine besondere und für unsere weiteren Überlegungen wichtige Situation, denn nun können wir für unterschiedliche Quantenzahlen gleiche Energiewerte erhalten:

E  =  h²/8ma² (n12 + n22 + n32)  =  h²/8ma²· K2  =  E1 · K2

wobei wir in der letzten Gleichung h²/8ma² durch E1 abgekürzt haben. Dies führt uns zu Betrachtungen über die Symmetrie und Entartung von Zuständen.


Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.