Der Kommutator verrät's !
Allgemeines Kriterium für die gleichzeitige Meßbarkeit:
Wir machen zunächst eine Messung, die die Meßgröße exakt bestimmen soll, d.h. mathematisch: Wir verlangen, dass die Wellenfunktion y nun Eigenfunktion zur Gleichung
(A ist wiederum der Operator für
die Meßgröße A, z.B. A
= h/i∂/∂x
für A = p)
Nun machen wir noch eine zweite Messung, die eine andere Meßgröße B exakt bestimmen soll. Wir verlangen daher, dass die Wellenfunktion y gleichzeitig Eigenfunktion zu
Ay = Ay und By = By
sein muss. Auf die erste Gleichung lassen wir links B und auf die zweite Gleichung A wirken; wir erhalten dann als Differenz:
BAy- ABy = ABy- BAy = ABΨ − BAΨ
(AB − BA)y = 0 · y
Damit ich zwei Größen A und B gleichzeitig messen kann, muss also für die entsprechenden Operatoren A und B gelten:
AB −BA = 0
Die Größe AB −BA wird als Kommutator bezeichnet und durch die eckigen Klammer [A, B] = AB− BA abgekürzt.
Impuls (p = h/id/dx)
und kinetische Energie (Ekin
= −h/2md²/dx²)
sind gleichzeitig scharf meßbar, da
(p . Ekin-
Ekin·p)y
= h/i(d/dx)·(−h/2md²/dx²)y-(−h/2md²/dx²)·(h/id/dx)y
= 0
Impuls (p) und Ort (x);
(px −xp)yº
(h/i.d/dx
x − x h/id/dx)y
= h/i(d/dx(xy)
−
x d/dxy)
= h/i(dx/dx·y
+ x dy/dx−
x dy/dx)
= h/iy
| [p, x]
= px −xp
= |
Folglich vertauschen Impuls- und Ortsoperator nicht miteinander und sind daher nicht gleichzeitig scharf meßbar.
Wir brauchen daher nur den Kommutator [A, B] derer Operatoren A und B bestimmen, um sagen zu können, ob die zugehörigen Meßgrößen gleichzeitig scharf meßbar sind.
Wir kennen bereits die Operatoren x,
t,
p,
H.
Den Drehimpulsoperator L erhalten wir über
die klassische Vektorbeziehung L = r´
p.
| klassisch | Operator |
| p = (px, py, pz) | p = |
| E = p²/2m + V | H = − |
| Lx = ypz − zpy | Lx = |
| Ly = zpx − xpz | Ly = |
| Lz = xpy − ypx | Lz = |
Für die gleichzeitige Meßbarkeit unterschiedlicher Größen erhalten wir das Ergebnis:
[E, t]
= i h
[Lx,
Ly]
= i h Lz
[Ly,
Lz]
= i h Lx
[Lz,
Lx]
= i h Ly
Die Komponenten des Drehimpulses sind also nicht gleichzeitig meßbar, jedoch kann man das Quadrat des Drehimpulses und eine Komponente gleichzeitig messen, denn es gilt:
[L2, Lj] = 0 j = x, y, z
Wie bereits gesagt brauchen wir nur den Kommutator [A, B] bestimmen, um sagen zu können, ob die zugehörigen Meßgrößen A und B gleichzeitig scharf meßbar sind, d.h. dass die "Fluktuationen" ΔA und ΔB verschwinden (gleich Null sind). Falls der Kommutator ungleich Null ist, dann gilt
(DA)²(ΔB)² ³ 1/4|<[A,B]>|².
Bisher haben wir uns nur dafür interessiert, ob dem Kommutator der Wert Null zukommt oder nicht. Bei späteren Problemen (der quantenmechnischen Beschreibung des harmonischen Oszillators) wird die Vertauschungsrelation wertvoll sein. Mit ihrer Hilfe kann in einer mathematischen Herleitung eine Verkettung AB von zwei Operatoren durch die Verkettung BA ersetzt werden.
Als Beispiel wird hier Vertauschungsrelation für die Operatoren a+ = −1/√2(d/dz+z) und a−= 1/√2(d/dz+z) hergeleitet. Wir gehen dazu vom Kommutator [a−,a+] aus.
| [a-,a+] | ||
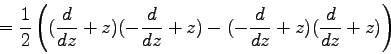 | ||
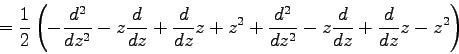 | ||
Der Wert des erhaltenen Operators offenbart sich, wenn er auf die Wellenfunktion ψ angewendet wird:
| [a-,a+]y | 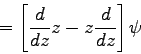 |
|
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.