Der harmonische Oszillator

Der harmonische Oszillator, bei dem die Rückstellkraft F proportional zur Auslenkung x aus dem Gleichgewicht ist, stellt eine gute Näherung für das Potential V(x) eines Moleküls dar. Da F ~ −d/dxV(x) ist, gilt für das Potential:

V(x)  =  ½ kx²

Der Hamilton-Operator und die Schrödingergleichung sind dann:

(−h²/2µd²/dx² + ½ kx²) y  =  E y

wobei µ die reduzierte Masse repräsentiert. Da wir Schreibarbeit einsparen wollen, führen wir die neuen Variablen z² = x²(kµ/h²)½ und ε = E/h(µ/k)½ = E/hw ein [w  =  (k/µ)½] und erhalten (d²/dx²  =  (kµ/h²)½d²/dz²) so:

½ (−d²/dz² + z²) y(z)  = E/hw  =  ε · y(z)  =  H y(z)

Wer sich nicht für den mathematischen Lösungsweg interessiert, kann hier gleich zum Ergebnis springen.

Wir versuchen nun den Term (−d²/dz² + z²) zu faktorisieren, wie z.B. bei −a² + b² = (−a + b) (a + b). Bei Operatoren ist dies natürlich nicht ganz so einfach, da wir sorgfältig auf die Reihenfolge achten müssen. Versuchsweise bilden wir
 

1/Ö2(−d/dz + z) 1/Ö2(d/dz + z)
|¾¾¯¾¾¾| |¾¾¯¾¾¾|
a+ a−

a+a− y(z)  =  ½ (−d²/dz² + z²) y(z) + ½(−d/dz z + z d/dz)y(z)

mit    ½ (−d²/dz² + z²)  =  H     und     Hy  =  e y   erhalten wir:

a+a− y  =  ey + ½ (-y(z) − z d/dzy + z d/dzy)  =  (e-½)y

Dies ist nun unsere Gleichung für den harmonischen Oszillator. Für die weitere Behandlung des Problems werden wir auf die bereits hergeleitete Vertauschungsrelation für die Operatoren a− und a+ zurückgreifen. Ihr zufolge gilt a−a+ - a+a- = 1. So können wir nach Bedarf a−a+ durch a+a− ersetzen und umgekehrt.

Wir wenden den Operator a- auf unsere Oszillatorgleichung   a+a−ψ =  (ε−½)· ψ an:

a−a+ a-y  =  (e- ½) a-y

(a−a+ )(a-y)  =  (e- ½) (a-y)

(a+a− + 1) (a-y)  =  (e- ½)(a-y)

a+a− (a-y)  =  (e- 3/2)(a-y)

Wir erhalten also durch Anwendung des Operator a− auf die Wellenfunktion y wiederum eine Wellenfunktion (a−y), die der obigen Gleichung für den harmonischen Oszillator, a+a-y = (ε − ½) y, genügt, allerdings mit einem Eigenwert, der um 1 niedriger ist: (e- ½)  →  (e-3/2). Der Operator a− senkt also den Eigenwert um 1 und wird Vernichtungsoperator genannt.

Da ε ein Maß für die Energie E ist (ε = E/hw) muss es einen niedrigsten Zustand yo geben. Wenden wir den Vernichtungsoperator auf yo an, dann würden wir einen noch tieferen Zustand erzeugen, was nicht sein darf! Also gilt für den niedrigsten Zustand

a− yo  =  0 und εo-½ = 0

εo  =  ½→  Eo  =  ½hw

Der niedrigste Zustand hat also die Energie ½hw. Berechnen wir nun die dazugehörige Wellenfunktion:

a− yo = (d/dz + z) yo  =  0      →  dyo/dz  =  −z yo   →     dyo/yo  =  −zdz     →     ln yo  =  −z²/2 + Konstante

yo  =  Co e−z²/2

Co wird durch die Normierung -¥ò+∞yo* yo dz = 1 festgelegt:

Co  =  p-¼

Nun wenden wir a+ auf unsere Gleichung a+a-y = (ε − ½) y an:

a+ (a+a-)y  = (e- ½) a+y

a+ (a−a+− 1) y  =  (e-½) a+y

a+a− (a+y)  =  (ε + ½)(a+y)

Durch Anwendung von a+ auf y erhöht sich der Eigenwert um 1. a+ wird daher Erzeugungsoperator genannt. Wenden wir a+ auf den niedrigsten Zustand yo an, dann erhalten wir die Wellenfunktion y1, die Eigenfunktion zum nächst höheren Eigenwert ist:
 

y1  =  a+yo

y1  =  C1 (−d/dz + z) · e−z²/2

y1  = C1 2z · e−z²/2

Der zugehörige Energiewert ist:
E1  =  3/2hw

y2  =   a+y1  =  C2 (−d/dz + z) z ·  e−z²/2

y2  =  C2(2z² − 1) e−z²/2

E2  =  5/2hw

usw. usw.

Ganz allgemein erhält man für die n. Wellenfunktion yn

yn  =  Cn (a+)n yo


Ergebnis:

Allgemein gilt für die möglichen Energieniveaus:
 

  En  =  hw (n + ½)        n = 0, 1, 2, .... 

Die Energie des Grundzustandes Eo = ½ hw bezeichnet man als Nullpunktenergie. Für die Wellenfunktion des n-ten Zustandes erhält man allgemein
 

yn(z)  =  Cn Hn(z) e−z²/2

wobei die Konstante Cn über die Normierungsbedingung -¥ò+∞yn* yn dz = 1 bestimmt wird:
 

Cn  =  1/(π½n!2n )½

und die Funktion Hn(z) bezeichnet man als Hermitesche Polynome:
 

H0(z)  =  1
H1(z)  =  2z
H2(z)  =  4z2 − 2
H3(z)  =  8z3 − 12z
H4(z)  =  16z4 − 48z2 + 12
H5(z)  =  32z5 − 160z3 + 120z
H6(z)  =  64z6 - 480z4 + 720z2 − 120

Genug: Alle anderen kann man sich aus der Rekursionsformel
 

Hn(z)  =  2z Hn−1(z) − 2(n−1) Hn−2(z)
ausrechnen.

z.B. um H3(z) zu bekommen, muss ich für Hn−1(z) ® H2(z) und für Hn−2(z) ® H1(z) einsetzen:

H3(z)  =  2z · (4z2−2)− 2(2) (2z)  =  8z3 − 12z
 

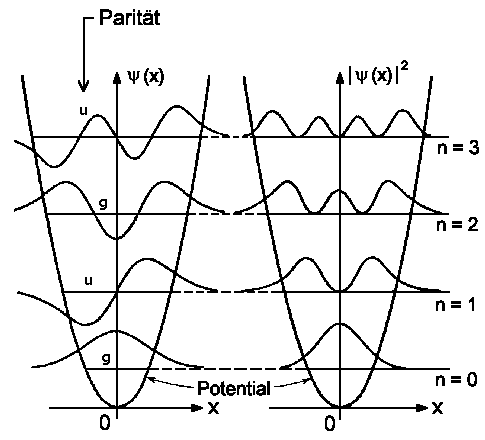Abb. 1: Die vier niedrigsten Wellenfunktion und deren Wahrscheinlichkeitsdichte für den harmonischen Oszillator.

\includegraphics[angle=-90,width=0.9\textwidth]{graphs/osz_properbility.eps}Im Grundzustand ist die größte Aufenthaltswahrscheinlichkeit in der Gleichgewichtslage (s. Abb. 1 für n=0). Mit zunehmender Vibration wird |yn|2 immer größer im Bereich der klassischen Umkehrpunkte E = V(x); s. Abb. links für n=5, 10, 20.

Wie groß ist bei einem klassischen Oszillator die Wahrscheinlichkeitsdichte das Teilchen im Intervall [x, x+dx] zu sehen?

klass. Oszillator:          x  =  xm sinwt               xm = maximale Auslenkung

In dem Zeitintervall dt (in der ich das Teilchen mir "ansehe") wird die Strecke dx zurückgelegt:

dx/dt  =  xmwcoswt

dt  =  dx/xmw coswt  =  dx/xmw (1−sin²wt)½

dt  =  dx/w (xm²−x²)½

Die Größe 1/w(xm²−x²)½ gibt die Wahrscheinlichkeitsdichte an, das Teilchen im Intervall [x, x+dx] zu finden; d.h. die größte Chance liegt bei den klassischen Umkehrpunkten xm vor. Wir finden also wieder, dass mit zunehmender Quantenzahl eine klassische Beschreibung erreicht wird.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.