Molekülschwingungen einfach gemacht:
Der harmonische Oszillator


Die potentielle Energie eines zweiatomigen Moleküls hat in einer gewissen Entfernung ein Minimum. Die Entwicklung der potentiellen Energie V(x) in eine Potenzreihe bezüglich der Gleichgewichtslage x0(für die dV(x)/dx|x0 = 0 ist) führt zu V(x) = V(0) + ½ d²V(x)/dx²|x0 x2. Wählen wir als Nullpunkt der Energiezählung V(0) und kürzen die Konstante d²V(x)/dx²|x0 mit k ab, dann erhalten wir als Näherung für das Potential

V(x)  =  ½ kx²          (x mißt Auslenkung aus Gleichgewicht)

Die Schrödingergleichung ist dann

(−h²/2md²/dx² + ½ kx²) y  =  E y

Da A und B gegeneinander schwingen, müssen wir noch m durch die reduzierte Masse µ = mAmB/mA+mB ersetzen.
Führen wir die neue Abstandsvariable z² = x² √(kµ/h²) ein, dann erhalten wir schließlich die Schrödingergleichung für die Schwingung:

(−d²/dz² + z²) y(z)  = 2 E/hw·y(z)

wobei die Schwingung durch die Kreisfrequenz ω charakterisiert wird. Diese ist beim Harmonischen Oszillator durch ω =√(k/μ) mit der Kraftkonstanten k und der reduzierten Masse μ verbunden. Wer sich für einen netten und zukunftsweisenden mathematischen Lösungsweg interessiert, kann ihn hier finden.


Ergebnis:

Allgemein gilt für die möglichen Energieniveaus:
 

En  =  hw (n + ½)

wobei n die ganzzahligen Werte n = 0, 1, 2, .... annehmen kann.

Die Energie des Grundzustandes Eo = ½ hw bezeichnet man als Nullpunktenergie. Für die Wellenfunktion dieses energetisch niedrigsten Zustandes erhält man eine Gaußfunktion:

yo(z)  = p-¼ e−z²/2

Im Grundzustand ist danach die größte Aufenthaltswahrscheinlichkeit in der Gleichgewichtslage (bei z=0). Für die Wellenfunktion des n-ten Zustandes erhält man allgemein
 

yn(z)  =  Cn Hn(z) e−z²/2

wobei die Konstante Cn über die Normierungsbedingung -¥ò+∞yn* yn dz = 1 bestimmt wird:
 

Cn  =  1/(π½n!2n )½

und die Funktionen Hn(z) bezeichnet man als Hermitesche Polynome:
 

H0(z)  =  1
H1(z)  =  2z
H2(z)  =  4z2 − 2
H3(z)  =  8z3 − 12z
H4(z)  =  16z4 − 48z2 + 12
H5(z)  =  32z5 − 160z3 + 120z
H6(z)  =  64z6 - 480z4 + 720z2 − 120


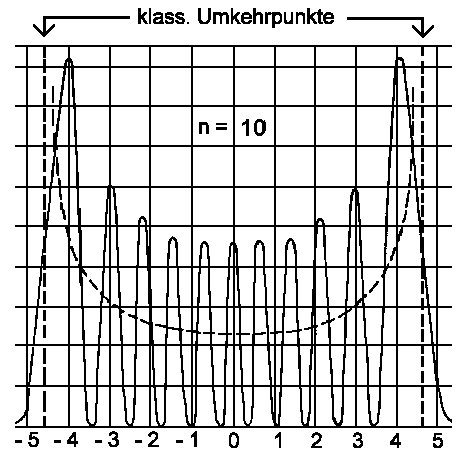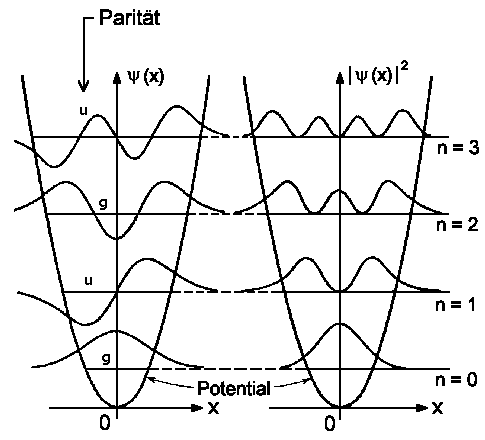
In der Spektroskopie hat es sich eingebürgert, die Quantenzahlen für die Vibration mit dem Buchstaben v (statt n) zu kennzeichnen, so dass dann die Energieniveaus durch Ev = hw (v + ½) mit v = 0,1,2,... beschrieben werden. Inhaltlich ändert sich dadurch natürlich gar nichts.

 
Wellenfunktion (links) und Aufenthaltswahrschein- lichkeit (rechts) für die vier niedrigsten Schwingungs- zustände.  Aufenthaltswahrscheinlichkeit für den Schwingungszu- stand n=10. Die gestrichelte Kurve gibt die klassische Aufenthaltswahrscheinlichkeit wieder. 

Im Grundzustand ist die größte Aufenthaltswahrscheinlichkeit in der Gleichgewichtslage. Mit zunehmender Vibration wird |yn|2 immer größer im Bereich der klassischen Umkehrpunkte E = V(x).
Der Verlauf der Wahrscheinlichkeitsdichte bei einem klassischen Oszillator ist durch  1/w(xm²−x²)½ gegeben. Diese Größe (s. gestrichelte Kurve in der rechten Abbildung) gibt die Wahrscheinlichkeitsdichte an, das Teilchen im Intervall [x, x+dx] zu finden; d.h. die größte Chance liegt bei den klassischen Umkehrpunkten xm vor. Wir finden also, dass mit zunehmender Quantenzahl eine klassische Beschreibung erreicht wird.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.