Der Tunneleffekt


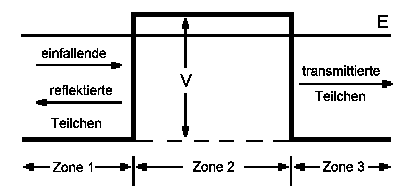
Wir betrachten ein Teilchen der Masse m, das mit der Energie E von links auf die Potentialbarriere der Breite a zufliegt. Klassisch ist völlig klar, was passiert: Wenn die Energie E des Teilchens kleiner als die Höhe der Potentialbarriere V ist, dann wird es reflektiert. Nur wenn die Energie größer als V ist, dann wird es die Barriere überwinden.  Die Quantenmechanik liefert hier einige Überraschungen. Die Schrödingergleichung zerfällt in drei Gleichungen, die für jeweils eine der drei Zonen gelten. Im Übergangsbereich, d.h. an den Kanten der Potentialbarriere müssen die Lösungen der drei Gleichungen jeweils stetig ineinander übergehen. Dasselbe muss auch für die Steigung (1. Ableitung) der Wellenfunktionen gelten. Das Quadrat der Wahrscheinlichkeitsamplitude für das nach rechts fliegende transmittierte Teilchen geteilt durch das Quadrat der Wahrscheinlichkeitsamplitude für das von links einfallende Teilchen ergibt die Transmissionswahrscheinlichkeit T (Herleitung):
 

 T  =  {1 + sinh2(ka)/[4 E/V (1-E/V)]}-1      mit  k  =  (2m(V-E)/h²)½ 

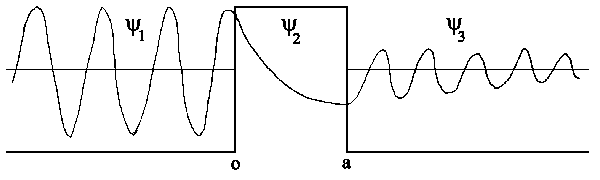
Obwohl E < V ist, ist  die Transmissionswahrscheinlichkeit T ungleich Null, d.h. das Teilchen tunnelt durch die Potenzialbarriere, was klassisch verboten ist. Die Wellenfunktion fällt nicht abrupt auf Null an der Stelle x = 0, da V nicht unendlich hoch und breit ist. Für ka > 1 gilt näherungsweise:
 

T  ≈  16E/V² (V − E) e−2ka

In der nachfolgenden Abbildung ist die Tunnelwahrscheinlichkeit T für unterschiedliche Energien E pro Potentialhöhe V aufgetragen. Dabei wurde als Beispiel ein idealisiertes Potential der H-Fragmentierung beim H-N3 im angeregten Zustand gewählt.
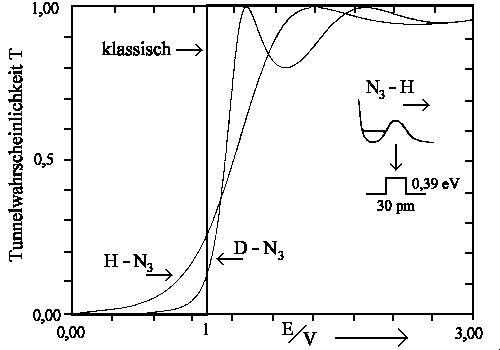Tunnelwahrscheinlichkeit für (stark vereinfachtes) H-N3 und D-N3 im elektronisch angeregten Zustand. Klassisch ist T = 0 für E/V<1 und T = 1 für E/V>1.
Die Potentialbreite a beträgt 30 pm, die Höhe V = 0,39 eV ≡ 37,6 kJ/mol. Die Tunnelwahrscheinlichkeit ist stark massenabhängig, wie die Substitution des H-Atoms durch Deuterium zeigt.


Für E > V kann T < 1 sein, d.h. Teilchen werden reflektiert, obwohl ihre Energie ausreicht, das Potential zu überwinden. Hier gilt (sinh durch sin ersetzen):

T  =  [1 - sin² k'a/4 E/V (1 − E/V)]-1  mit  k'  =  (2m(E-V)/h²)½
 

P.S. Für E = V erhält man (nach l'Hopital):

T  =  [1 −ma²V/2h²]-1

Eine technische Anwendung des Tunneleffekts ist das Rastertunnelmikroskop.

 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.