Die Energiezustände und die radiale Wellenfunktion R(r)
des Wasserstoffatoms


Ausgangspunkt ist unsere DGL für R(r), die wir vor Ableitung der Drehimpulsquadrats-Eigenfunktion Yl,m(J,j) gewonnen hatten:

[−h²/2µ 1/r² ∂/∂r(r² ∂/∂r) + V(r) + h²l(l+1)/2µr²− E] R(r)  =  0

Für das Potential eines Elektrons im Z-fach geladenen Kern gilt V(r) = −Ze²/4peo1/r . Multiplikation mit −2µ/h² ergibt:

 d²/dr² R + 2/r dR/dr + [2µE/h² + 2µ/h²Ze²/4peo1/r−l(l+1)/r²] R  =  0

Zur einfacheren Schreibweise führen wir nun einige Abkürzungen ein und kennzeichnen die Ableitungen durch Striche (R'  ≡d R/dr ):

ρ  =  2 ε r          B  = Ze²µ/4peoh²ε     ε²  =  −2µE/h²     (Bindungsenergie)

R'' + 2/ρ R' − [¼ − B/ρ + l(l+1)/r ²] R  =  0

Für große Entfernungen (ρ →∞) entfallen alle 1/r ,1/r ² -Terme:

R'' − R/4≈  0     →     R(ρ)  =  C e−ρ/2     oder     R(ρ)  =  C e+ρ/2

Die zweite Lösung entfällt, da dann R(ρ) im Unendlichen nicht beschränkt ist, sondern unendlich groß wird.
Die detaillierte Lösung steht auf einem anderen Blatt; hier die Kurzform:
Mit dem Lösungsansatz

R(ρ)  =  e−ρ/2.ρl Σk=0 ck ρk

gehen wir in die DGL und vergleichen die Koeffizienten von ρk (die DGL muss für jedes r und daher jedes ρk gelten), dann erhält man:

ck+1/ck  = (l + k + 1 −B)/(k + 1)(k + 2l + 2)

Die Reihe beginnt bei k = 0. Sie muss irgendwo abbrechen, damit R nicht über alle Grenzen wächst, d.h. es muss ein Koeffizient Null werden:
 

l + k + 1 − B  =  0
½¾¯¾½
n

l, k, 1 sind ganze Zahlen, d.h. n = l + k + 1 muss eine ganze Zahl sein
 

n  =  1, 2, 3, 4 ... 

0  ≤  l  ≤  n −1

 da l, k = 0, 1, 2, 3.... 

n wird Hauptquantenzahl genannt

Einsetzen der Abkürzungen für B = n ergibt:
 

En  =  −µ/2(Ze²/4peoh)².1/n²

Die Energie ist also gemäß der Hauptquantenzahlen n quantisiert; die möglichen Werte für den Drehimpuls sind l = 0, 1, 2, ..., n−1 und für jedes l gibt es (2l+1) m-Werte.

Für n = 1 ist l = 0, k = 0       →          R(ρ)  =  C e−ρ/2

oder nach Einsetzen für r = (2Z/aon) r :    R(r)  =  C e−Zr/nao

mit der Abkürzung (Bohrscher Radius)    ao  =  4peoh²/µe²

Das Polynom Σ ckρk im Lösungsansatz R(ρ) = e−ρ/2.ρlΣk=0 ckρk   wird als assoziiertes Laguerresches Polynom(Σk=0 ckρk ≡  Ln-l-12l+1(ρ)) bezeichnet. Häufig gibt es ab hier ein heilloses Durcheinander, da in manchen Lehrbüchern die Laguerrschen Polynome etwas anders definiert sind. Wir halten uns hier an die mathematische Form, die auch das Programmpaket "Mathematica" benutzt. Und so lässt sich jedes beliebige assoziierte Laguerrsche Polynom Lpq(x)  berechnen (Rodrigues Darstellung):

Lpq(x)  =  ex x-q/p!. dp/dxp (e-xxp+q)

Für Mathematica-Besitzer ist es ganz einfach. Die nachfolgende Programmzeile druckt die ersten 5 assozierten Laguerreschen Polynome (wer höhere Polynome sehen möchte, ersetze 5 durch die höhere Zahl):
Do[Print[ "n=",n," l=",l,"  " , LaguerreL[n-l-1,2l+1,x]],{n,1,5},{l,0,n-1}]
Die Tabelle der niedrigsten Polynome zeigt, dass dies wirklich einfache Funktionen sind:
 

Elektron n l Ln-1-12l+1 (x)
1 s 
2 p 
3 d 
4 f 
 1 
2 
3 
4 		 0 
1 
2 
3 		 1 
1 
1 
1 
2 s 
3 p 
4 d 		 2 
3 
4 		 0 
1 
2 		 2 - x 
4 - x 
6 - x 
3 s 
4 p 		 3 
4 		 0 
1 		 6 - 6x + x²
20 - 10x + x²
4 s  4  0  24 - 36x + 12x² - x³

Die gesamte Lösung für den Radialanteil der Wellenfunktion nimmt dann die Form
 

Rn,l  =  Cn,l ·ρl. e−ρ/2 Ln-1-12l+1(ρ)

an, wobei die Konstanten Cn,l (nicht zu verwechseln mit den Koeffizienten ck unserer Reihenentwicklung) noch als Normierungsfaktor festgelegt werden muss. Diese ergeben sich aus der Normierungsbedingung:
 

oò¥ Rn,l · Rn,l · r² dr  =  1

Wenn wir jetzt ρ durch r ersetzen, r = (2Z/aon) r, dann ergibt sich als vollständige Lösung:
 

Rn,l  =  {4(n−l−1)! Z³/[(n+l)!]n4ao³}½ (2Zr/nao)l e−Zr/nao Ln-l-12l+1(2Zr/nao)

wobei wir wieder

ao  =  2 r Z/n ρ  =  h²(4peo)/µe²
verwenden.
Die Anzahl der Gleichungen für den Radialanteil entspricht nahezu der Anzahl an Lehrbüchern. Es gibt kaum ein Lehrbuch, das nicht in irgendeiner Weise eine Gleichung falsch angibt. Wer keinen Fehler machen möchte, kann sich die Gleichungen selbst mit "Mathematica" ausrechnen, wobei der Abstand r in Einheiten von ao gemessen wird (z.B. r=2 entspricht 2ao = 0,112nm) :
Rnl[n_,l_]:= 2*Sqrt[z^3/n^4*(n-l-1)!/(n+l)!]*(2*Z*r/n)^l*Exp[-Z*r/n]* LaguerreL[n-l-1,2l+1,2*Z*r/n]
nmax=5; Do[Print[ "n=",n," l=",l,"  " ,Rnl[n,l]],{n,1,nmax},{l,0,n-1}]

Die Wellenfunktionen Rn,l(r) und die Wahrscheinlichkeit das Elektron in der Entfernung r vom Kern zu finden, Rn,l2r2 sind in der nachfolgenden Abbildung dargestellt:
 

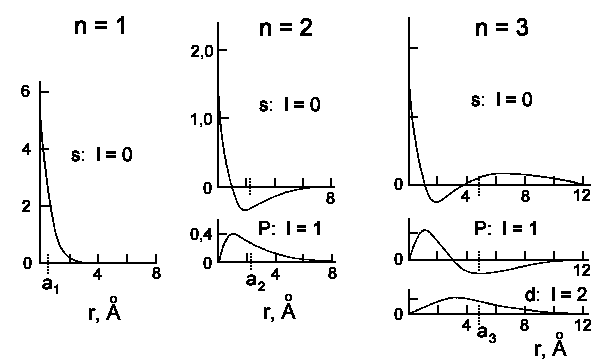Radiale Wellenfunktionen von Wasserstoff für n = 1, 2 und 3. Die Ordinate ist immer 
[Rn,l(r) m−3/2]·10−8.
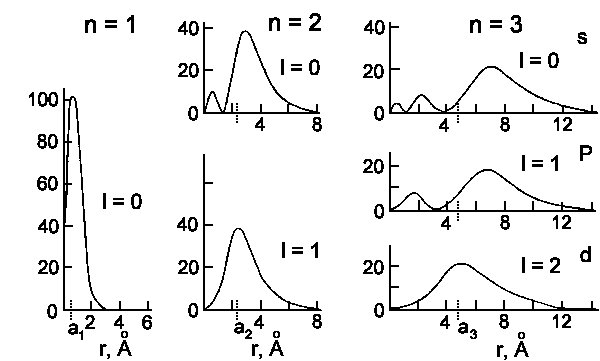Radiale Wahrscheinlichkeit im Wasserstoff für n = 1, 2, and 3.

Darstellungen der Gesamtwellenfunktion y(r,J,j) = R(r) .Y(J,j)  für wasserstoffähnliche Atome findet man im nächsten Kapitel.
 


Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.