Quanta

Newton described light according to his conception of light as a particle (Quanta). Christiaan Huygens, however, in 17th century introduced the idea of waves to describe the properties of light. The wave nature of light has further been seen by using diffraction experiments such as the double slit experiement by Thomas Young in 1801. These experiments provide indisputable evidence of the wave-like nature of light. Max Planck's Black Body Theory also hints at the wave-like nature of light but it did not resolve all questions that scientists had at the time. Later, more pivotal experiments were conducted that proved the discreet "quantum-like" nature of EM radiation. There were, however, still indications that light also has a particle-like nature. Thus resulted the wave-particle duality that is our most current understanding of light. We would like to exhibit a few experiments which distinctly prove the particle features of light: the photoeffect and the Compton effect:


The Photoeffect


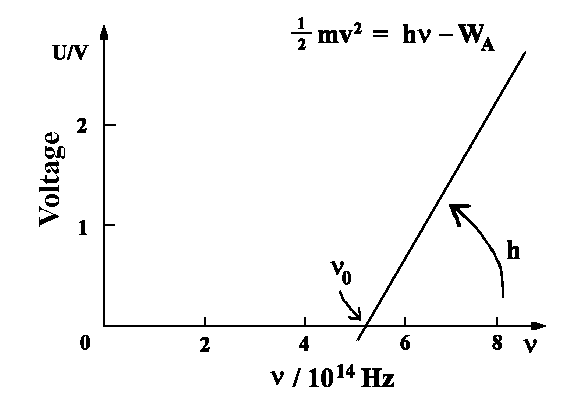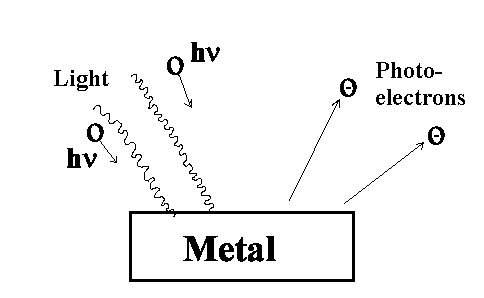
If electromagnetic radiation with a high frequency strikes a metal surface, electrons will be emitted. These electrons are referred to as photoelectrons. This process is called the photoelectric effect.

Classical description:
The energy E of the incident light particle transfers enough energy to free electrons from the metal nucleud. Electrons in different atoms require different amounts of energy to break free from their respective atoms. It turns out that increasing the aplitude of the incident light "wave" particles doesn't increase the likelyhood that an electron will be released.

Experiment:
There are no photoelectrons observed below frequency νo .
The electron velocity doesn't depend on the light power.
The photoelectrons are also immediately emitted when applying weak light power.

Quantum description:
The amount of energy hν is absorbed. Since the electron is bound to the metal, the photon must have at least enough energy in order to break free from the molecule WA. The rest of energy will be contained in the kinetic energy of the photoelectron.
 

½ me v2  =  hn- WA

  WAOne can find the photoeffect applied in the use of photomultipliers. The avalanche amplification of emitted photoelectrons is used even for the detection of single photons (photon counting regime). It's detects one photon out of about 3 photons on average. The human eye is also quite sensitive after a long accomodation period: some 10 photons per second are enough to see a light.
 

Light as Billiards Ball: The Compton Effect

The Compton effect is the most conclusive evidence of a particles electromagnetic behavior. 
 
 

Experiment:
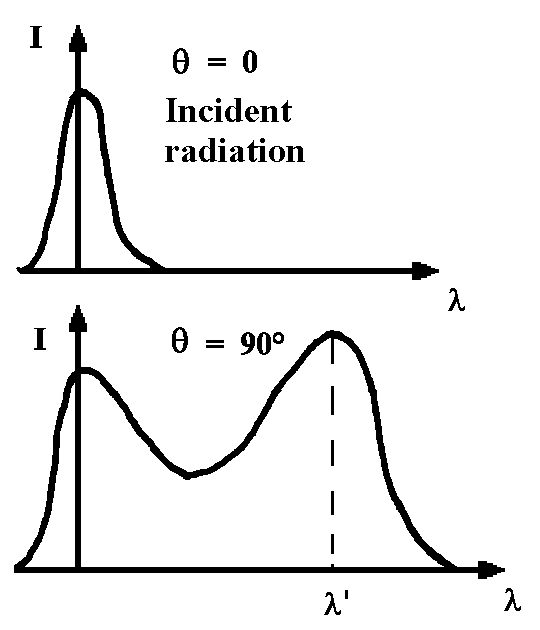
The Roentgen beams fall on graphite and then diffract in all directions. The diffracted radiation has a component with the same frequency as the incident emission whereas other components have a lower frequency. The frequency increases with a larger angle θ.

Energy conservation:
Energy before collision = Energy after collision :

hν  +  m0c2  =  hν’ +  mc2

hn  −  hν’  =  mc2  −  m0c2

ν  -n'  =  m0c²/h{[1/(1 − v²/c²)½]− 1}

where we used the Einstein expression mc2 = moc2/(1 -n2/c2)½ .
The photon transfers its energy to an electron and therefore its frequency decreases (ν’ <n).

Impulse conservation:
Photon has an impulse since after Einstein:

E  =  mc2  =  p · c  =  hν  =  hc/λ

p  =  h/l            p  =  hν/c

 
Impulse  p = h/cν' ; px = h/cν' · cosθ
Impulse  p = m · v ; px = m · v · cosj

 1/ν'  =  1/ν  +  h/m0c²(1 − cosθ)

λ'  =  λ  + h/moc (1  -  cosθ)

The quantity  h/moc is the Compton wavelength and it is equal to 0,00243 nm.

The maximum wavelength change can be detected for θ = 180° (backwards diffraction).

Dlmax  =  λ' - l  =  0,00486 nm      (it doesn't depend on the wavelength)

Classically there is no any wavelength change, since  h = 0 !

The predictions are proved by an experiment:

Summing up all these experiments one can say:  The Photon also behaves like a particle !

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.